Эта идея вряд ли принесет пользу, если вы в точности станете следовать ей на практике. Но некоторые художники поступали именно так, используя полупрозрачные материалы или стекло вместо полотна. Они часто применяли этот прием на подготовительном этапе, нанося набросок на полотно перед тем, как писать картину. Более практичным подходом было бы использовать эту концептуальную формулировку для связи геометрии трехмерной сцены с двумерной картинкой на полотне. Привычная нам евклидова геометрия работает со свойствами, остающимися неизменными при их перемещении: длиной и углами. Хотя сам Евклид не формулировал свои принципы именно так, его основной инструмент – конгруэнтные треугольники – производит такой же эффект (имеются в виду треугольники одинаковой формы и размеров, но расположенные в разных местах). Точно так же геометрия перспективы сводится к свойствам, которые остаются неизменными при проекции. Легко заметить, что длины и углы не ведут себя так же. Вы можете прикрыть Луну одним пальцем – получается, длина способна меняться? С углами еще хуже: если вы посмотрите на угол здания и он прямой, то он будет казаться прямым, только если вы посмотрите на него прямо.
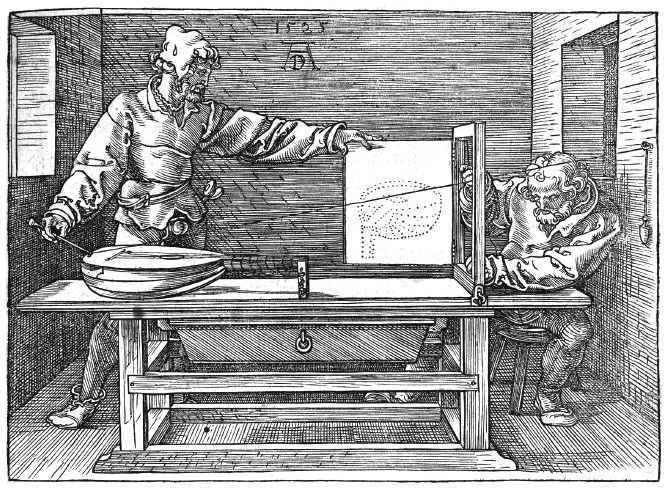
Проецирование картинки. Гравюра Альбрехта Дюрера
Какие же свойства геометрических фигур сохраняет проекция? Самые важные кажутся нам такими простыми, что трудно поверить в их значение. Точки остаются точками. Прямые – прямыми. Образ точки, расположенной на прямой, останется на изображении этой линии. Получается, если две линии встречаются в какой-то точке, их изображения тоже встречаются в соответствующей точке. Отношения между точками и прямыми сохраняются в проекции.
Важной чертой, не полностью сохраняемой в проекции, является взаимодействие параллельных прямых. Представьте, что вы стоите посреди бесконечно длинной прямой дороги и смотрите вперед. Две ее стороны, параллельные друг другу в трехмерной реальности (никогда не встречающиеся), уже не выглядят параллельными. Они сходятся в одну точку где-то у горизонта. Они всегда ведут себя так, как будто находятся на идеально бесконечной плоскости, а не слегка скругленной Земле. По сути, они и могут вести себя так только на плоскости. На сфере будет едва заметный разрыв, слишком маленький, чтобы его рассмотреть, там, где линии пересекают горизонт. Получается, все рассуждения о параллельных линиях на шаре весьма запутанны.
Такая особенность параллельных линий очень полезна для изображения перспективы. Это основа привычного рисования прямоугольных объектов в перспективе, когда используются линия горизонта и две исчезающие точки там, где параллельные линии коробки пересекают перпендикулярный им край. «О перспективе в живописи» – труд Пьеро делла Франческа, изданный в 1482–1487 гг., – развил метод Альберти в практические приемы для художников. Сам живописец успешно применял свои идеи в создании драматичных и весьма реалистичных полотен.
Труды художников Возрождения разрешили многие проблемы в геометрии перспективы, но они оставались полуэмпирическими, страдая нехваткой логических обоснований, поддерживавших здание евклидовой геометрии. Эта проблема обоснований была в итоге решена Бруком Тейлором и Иоганном Генрихом Ламбертом в XVIII в. Но к тому времени в геометрии произошли еще более поразительные перемены.
Дезарг
Первую нетривиальную теорему в проективной геометрии открыл инженер-архитектор Жерар Дезарг. Ее опубликовал в своей книге в 1648 г. Абрахам Босс. Дезарг доказал следующую важную теорему: «Предположим, треугольники АВС и А´В´С´ находятся в перспективе. Это означает, что три линии, АА´, ВВ´ и СС´, проходят через одну точку. Тогда три точки P, Q и R, в которых пересекаются продолжения трех пар сторон треугольника, лежат на одной прямой». Этот результат теперь нам известен как теорема Дезарга. В ней не упоминаются ни длина, ни углы: она целиком посвящена отношениям между прямыми и точками. А значит, это и есть проективная теорема.
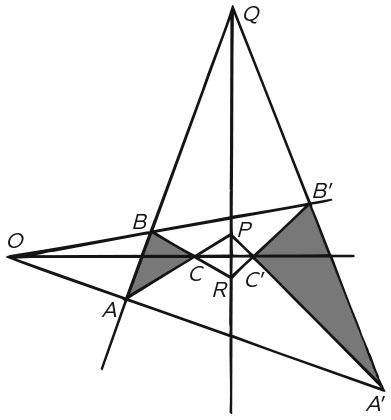
Теорема Дезарга
Есть одна хитрость, делающая теорему очевидной: представьте себе, что рисуете изображение трехмерной фигуры, у которой два треугольника лежат в двух плоскостях. Тогда на линии, по которой пересекаются эти плоскости, и будут расположены три точки Дезарга P, Q и R. Без особого труда так даже можно доказать эту теорему, построив соответствующую трехмерную фигуру, чьи проекции выглядят как два треугольника. Значит, мы можем использовать методы Евклида, чтобы доказывать проективные теоремы.
Аксиомы Евклида
Проективная геометрия отличается от евклидовой настолько, насколько близка вам такая точка зрения (каламбур намеренный!), но корнями она по-прежнему уходит в геометрию Евклида. Это исследования новых видов преобразований, т. е. проекций, но изначально модель пространства, подвергающегося преобразованию, принадлежит Евклиду. Тем не менее проективная геометрия в целом заставила математиков стать более восприимчивыми к возможности существования нового образа геометрического мышления. И старый вопрос, пролежавший под спудом целые века, снова стал актуальным.
Практически все аксиомы Евклида настолько очевидны, что ни одному человеку в здравом уме не придет в голову подвергать их сомнению. Например, аксиома о том, что все прямые углы равны. Если она неверна, значит, что-то не так с самим определением прямого угла. Но пятый постулат, касающийся параллельных прямых, имеет совершенно другой оттенок. Он слишком сложен. Вот как его формулировал сам Евклид: «И если прямая, падающая на две прямые, образует внутренние и по одну сторону углы, меньшие двух прямых, то продолженные неограниченно эти прямые встретятся с той стороны, где углы меньше двух прямых».
Звучит скорее как теорема, а не как аксиома. Было ли это теоремой? Может ли в таком случае быть у нее доказательство, исходящее из чего-то еще более простого, интуитивного?
Упростил формулировку постулата в 1795 г. Джон Плейфэр. Он выразил ее так: на плоскости через точку, не лежащую на данной прямой, можно провести одну и только одну прямую, параллельную данной. Эта аксиома логически эквивалентна пятому постулату Евклида: они являются следствием друг друга, при этом учитывают остальные аксиомы.
Лежандр
В 1794 г. Адриен-Мари Лежандр открыл еще одну эквивалентную формулировку постулата, в которой говорится о подобных треугольниках – фигурах, имеющих равные углы, но разные длины сторон. Однако он, как и большинство математиков того времени, предпочел бы что-то более интуитивное. Им казалось, что пятый постулат избыточен: это следствие из других аксиом, и что только для него упущено доказательство. И Лежандр перепробовал всё, что мог, чтобы доказать его. Используя только другие аксиомы, он доказал – для своего удовольствия, по крайней мере, – что сумма внутренних углов треугольника не превосходит 180°. (Ему наверняка было известно, что в сферической геометрии сумма больше, но ведь это геометрия сферы, а не плоскости.) Если сумма всегда равна 180°, то отсюда сразу логически вытекает пятый постулат. И он предположил, что сумма может быть меньше 180°, и построил свои рассуждения на этом.

