ЧТО ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДАЛИ ИМ
Предложенная Кеплером модель эллиптических орбит была не так точна. Она была бы надежной в случае двух тел в Солнечной системе, но уже появление третьего начинает менять (нарушать) эллиптическую орбиту. Огромные расстояния между планетами несколько смягчают это воздействие, отчего большинство орбит всё же остаются близкими к эллипсам. Но Юпитер и Сатурн ведут себя очень странно: то замедляются и не попадают вовремя в ожидаемую точку, то, наоборот, делают рывок вперед, опережая график. Этот эффект возникает из-за их взаимного притяжения, а также из-за притяжения к Солнцу.
Закон всемирного тяготения, открытый Ньютоном, не ограничивает число тел в системе, но вычисления по его формуле очень сложны, если тел три или больше. В 1748, 1750 и 1752 гг. Французская академия наук учреждала премии за точный расчет орбит движения Юпитера и Сатурна. В 1748 г. Эйлер с помощью дифференциальных уравнений описал, как притяжение Юпитера воздействует на орбиту Сатурна, и получил премию. Он повторил попытку в 1752 г., но на сей раз в его работу вкралось несколько серьезных ошибок. Однако идеи, заложенные им в основу метода в целом, оказались весьма полезны.

Юпитер и Сатурн, изображенные вместе
СОФЬЯ ВАСИЛЬЕВНА КОВАЛЕВСКАЯ 1850–1891

Софья Ковалевская была дочерью генерала артиллерии и могла гордиться благородным происхождением. Но случилось так, что стены ее детской были обклеены страницами лекции по математическому анализу. В 11 лет ее впервые заинтересовали странные обои, и девочка сама научилась основам исчисления. Она всерьез заинтересовалась математикой, предпочтя ее всем прочим наукам. Отец пытался воспрепятствовать такому странному увлечению, но ничего не смог поделать: девочка читала книги по алгебре, когда родители спали. Чтобы получить свободу передвижения и продолжить образование, ей пришлось выйти замуж, однако брак не был удачным. В 1869 г. она начала изучать математику в Гейдельберге, но, поскольку в этот университет не принимали женщин, Софья ценой немалых усилий получила разрешение слушать курсы лекций неофициально. Продемонстрировав недюжинный математический талант, в 1871 г. она перебралась в Берлин, где ее наставником стал выдающийся аналитик Карл Вейерштрасс. И снова ей не удалось стать полноправной студенткой, но Вейерштрасс давал ей частные уроки.
Она занималась собственными исследованиями, и к 1874 г. Вейерштрасс решил, что ее работа достойна докторской степени. Софья написала три статьи: о ДУЧП, эллиптических функциях и кольцах Сатурна. В тот же год ученая была удостоена докторской степени от Университета Гёттингена. Статья о ДУЧП опубликована в 1875 г.
В 1878 г. у Софьи родилась дочь, но уже в 1880 г. она вернулась в математику и стала изучать рефракцию света. В 1883 г. ее муж, с которым они давно жили раздельно, покончил с собой, а Софья всё глубже погружалась в математику в надежде заглушить чувство вины. Она получила место преподавателя в Стокгольмском университете в 1884 г. и читала там лекции. В 1889 г. она стала третьей женщиной, которой предложили стать профессором в европейском университете, после Марии Аньези (так и не решившейся занять этот пост) и физика Лауры Басси. Здесь Софья провела исследование о вращении твердого тела, выдвинула свою работу на конкурс, объявленный Академией наук в 1886 г., и выиграла. Жюри так восхитилось ее блестящей работой, что даже увеличило денежный приз. Следующая работа в той же области получила премию Шведской академии наук, а также стала поводом для избрания ее членом Императорской Санкт-Петербургской академии наук.
Обыкновенные дифференциальные уравнения
Мы посвятим этот раздел двум самым важным вкладам в применение ОДУ (обыкновенных дифференциальных уравнений) в механике. В 1788 г. Лагранж опубликовал свою «Аналитическую механику», с гордостью отметив во вступлении:
В этой работе нет чертежей. Излагаемые мною методы не требуют построений, геометрических или механических рассуждений, а только алгебраических действий, подчиненных регулярному и единообразному ходу.
К тому времени стали очевидны ловушки и недостатки наглядных доказательств, и Лагранж задался целью не прибегать к ним. Теперь схемы и рисунки снова были в деле, подкрепленные неопровержимой логикой и доказательствами, но упорство Лагранжа, решившего описать законы механики только формулами, дало бесценный толчок развитию новой области знаний. Любая система может быть описана с помощью самых разных переменных. Например, для маятника обычная координата – угол его отклонения, но расстояние по горизонтали от него до вертикали ничем не хуже.
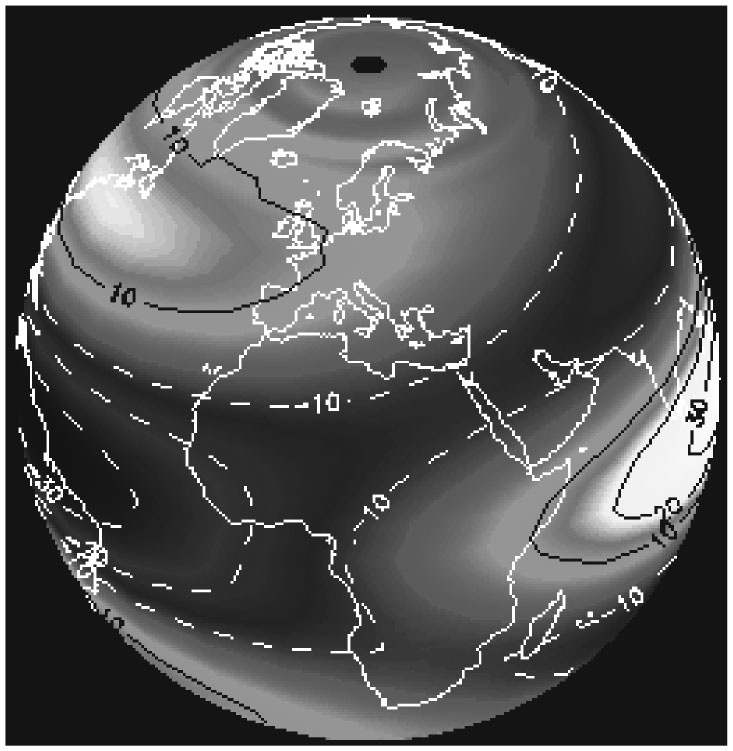
Скорость глобального ветра и колебания температуры, вычисленные по расширенной версии уравнений Навье – Стокса
Уравнения движения могут выглядеть совершенно по-разному в различных системах координат, и Лагранжу это казалось неэлегантным. Он нашел способ так переписать их, что они становились схожими для любой системы координат. Первым его изобретением стали парные координаты. Для каждой координаты q (такой, например, как угол отклонения маятника) существовала соответствующая ей координата скорости
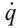 (угловая скорость движения маятника). Если имеется k координат положения, то будет и k координат скорости. Вместо дифференциальных уравнений второго порядка Лагранж вывел уравнения первого порядка по положению и скорости. Он сформулировал это в терминах величины, сейчас называемой лагранжианом.
(угловая скорость движения маятника). Если имеется k координат положения, то будет и k координат скорости. Вместо дифференциальных уравнений второго порядка Лагранж вывел уравнения первого порядка по положению и скорости. Он сформулировал это в терминах величины, сейчас называемой лагранжианом.
Уильям Гамильтон развил идеи Лагранжа, сделав их еще более элегантными. Физически он использовал импульс вместо скорости, чтобы определить дополнительные координаты. Математически он вычислил величину, известную сейчас как гамильтониан, или функция Гамильтона, которую можно интерпретировать – для многих систем – как энергию. В теоретических работах по механике, как правило, используется формализм Гамильтона, оказавшийся актуальным и для квантовой механики.
ЧТО ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДАЮТ НАМ
Между волновым уравнением и современными радио и телевидением есть самая прямая связь.

