Трудные времена. 1611-й был плохим годом. У Кеплера умер семилетний сын. Следом ушла жена. Император Рудольф, не притеснявший протестантов, отрекся от престола, и Кеплеру пришлось покинуть Прагу. В 1613 г. он женился во второй раз, и вопрос, который возник у него во время свадебных торжеств, привел к написанию книги «Новая стереометрия винных бочек» (1615).
В 1619 г. ученый опубликовал продолжение «Тайны мироздания». Эта книга отражает богатство новой математики, в ней много рисунков, похожих на плиточные узоры, а также многогранников. Во время работы над книгой ему сообщили, что его мать обвинили в колдовстве. При помощи факультета права Университета Тюбингена женщину удалось освободить, отчасти благодаря тому, что дознаватели не успели прибегнуть к предписанным в таком случае пыткам.
Коперник
Масла в огонь подлили в 1543 г., когда польский ученый Николай Коперник опубликовал поразительную, оригинальную и в чем-то еретическую книгу «О вращении небесных сфер». Как и Птолемей, для точности он использовал эпициклы. В отличие от Птолемея, в центр он поместил Солнце, а все остальные небесные тела, в том числе Земля (за исключением Луны), вращались вокруг него. Только Луна ходила вокруг Земли.
Главная причина такого радикального предположения Коперника была вполне прагматичной: вместо 77 эпициклов Птолемея у него оставалось всего 34. Среди эпициклов Птолемея встречалось много повторяющихся окружностей: то и дело обнаруживались фигуры одного и того же размера и скорости вращения, описывающие многие отдельные тела. Коперник обнаружил, что если все эти эпициклы приписать Земле, достаточно всего одного из них. Сейчас мы интерпретируем это в терминах движения планет относительно Земли. Если мы ошибочно предположим, что Земля неподвижна, как может показаться неискушенному наблюдателю, то ее движение вокруг Солнца как раз и придется переносить на другие планеты при помощи того самого дополнительного эпицикла.
Еще одним преимуществом теории Коперника стало то, что он придал всем планетам равный статус. Птолемею понадобились различные механизмы, чтобы описать движение планет, внутренних и внешних. Теперь же единственным отличием оставалось то, что внутренние планеты ближе к Солнцу, чем Земля, а остальные – дальше. Всё это выглядит очень логично и стройно – но было безоговорочно отвергнуто всеми учеными по многим причинам, не только религиозным.
Теория Коперника оказалась сложной, непривычной, а его книга – трудной для прочтения. Тихо Браге, один из лучших астрономов того времени, обнаружил несовпадения между гелиоцентрической теорией Коперника и отдельными мелкими данными, не совпадавшими и с теорией Птолемея. Он попытался найти разумный компромисс.
Кеплер
Когда Браге умер, его научное наследие досталось Кеплеру, который потратил многие годы на поиск закономерностей в изобилии данных. Кеплер был последователем мистической пифагорейской традиции и пытался притянуть к имевшимся у него данным откровенно искусственные объяснения. Самой известной из этих бесплодных попыток найти закономерности в небесах стало его изящное, но ошибочное описание пространственного расположения планет с точки зрения платоновых тел. В его время ученым были известны шесть планет: Меркурий, Венера, Земля, Марс, Юпитер и Сатурн. Кеплер задался вопросом, нельзя ли описать расстояния от них до Солнца с помощью геометрической модели. Более того, он задумался, почему планет именно шесть. Он обнаружил, что они явно оставляют место еще для пяти промежуточных форм, а поскольку геометрия описывала ровно пять правильных тел, это и ограничивает число планет шестью. Он предложил для них шесть сфер, где каждая несет орбиту на своем экваторе. А между ними, точно снаружи от одной сферы и внутри следующей, он разместил пять правильных тел в таком порядке:

Все числа хорошо совпадали, особенно если учесть ограниченные возможности астрономов того времени. Но существовало 120 различных способов разместить пять правильных тел, так что пространство в промежутках могло иметь разные размеры. Ничего удивительного, что один из этих вариантов оказался поразительно близок к реальности. Позже открытие новых планет нанесло роковой удар по всей теории, превратив ее в очередную тупиковую ветвь.
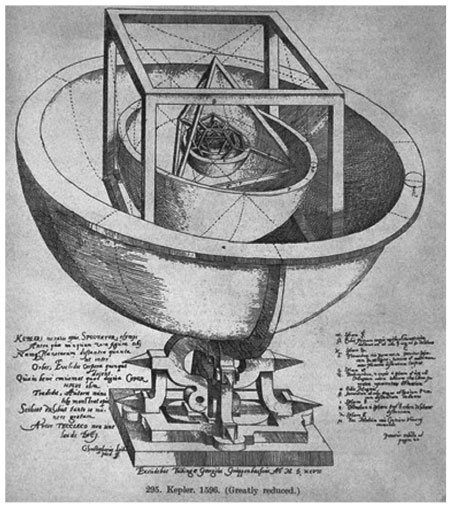
Теория Кеплера о расположении планетарных орбит
Однако в ходе своих исследований Кеплер открыл несколько законов, благодаря которым мы заслуженно считаем его гением. Эти законы Кеплера ученый установил интуитивно, исходя из анализа данных, собранных Тихо Браге. Вот как они звучат.
1. Все планеты Солнечной системы обращаются по эллипсам.
2. За равные промежутки времени радиус-вектор, соединяющий Солнце и планету, описывает равные площади.
3. Квадраты периодов обращения планет вокруг Солнца относятся как кубы больших полуосей орбит планет.
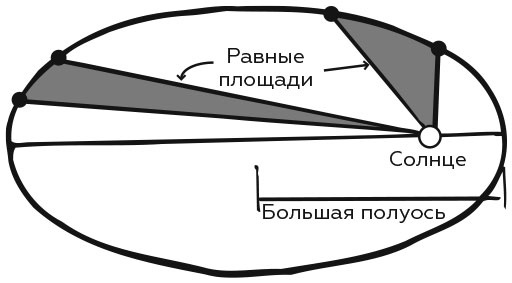
Движение планеты за равный промежуток времени
Самой оригинальной чертой работы Кеплера был отказ от классической окружности (якобы единственно возможной самой совершенной формы) в пользу эллипса. Этот шаг дался ученому с большим трудом, только когда он твердо убедился, что всё остальное не удовлетворяет его требованиям. У Кеплера не было оснований надеяться, что три закона будут точнее отражать реальность, чем гипотеза, основанная на платоновых телах, но это случилось. Три закона Кеплера имеют неоценимое значение для науки.
Галилей
Следующей выдающейся фигурой той эпохи стал Галилео Галилей, открывший математические формулы движения маятника и падающих тел. В 1589 г., занимая должность профессора математики в Пизанском университете, он проводил эксперименты по качению шара по наклонной плоскости, но не опубликовал результаты. Однако именно тогда он осознал важность контролируемого эксперимента для изучения законов природы: эта идея стала фундаментальной для науки. Он занимался астрономией и сделал несколько важных открытий, побудивших его признать теорию Коперника о гелиоцентрической планетарной системе. Это обострило его отношения с церковью, обвинившей ученого в ереси и посадившей под домашний арест.
В последние годы жизни, уже окончательно ослабев здоровьем, Галилей создал «Беседы и математические доказательства двух новых наук», где объясняется его работа по движению тел на наклонных плоскостях. Он утверждал, что расстояние, на которое прокатится с постоянным ускорением изначально неподвижное тело, пропорционально квадрату времени. Основой его закона стало более раннее открытие, что снаряд летит по параболе. В сочетании с законами Кеплера о движении планет это заложило основу новой области науки – механики, математического описания движения тел.

