Большая часть утверждений, которые мы можем доказать, относится к кривым рангов 0 и 1. Если ранг равен 0, то существует конечное число рациональных решений. Если ранг равен 1, то одно конкретное решение позволяет получить почти все остальные, за исключением, возможно, конечного числа решений. Эти два случая включают все эллиптические кривые вида y² = x³ + px, где p — простое число вида 8k + 5 (такое, как 13, 29, 37 и т. д.). Предполагается, что в этих случаях ранг всегда равен 1, что подразумевает существование бесконечного числа рациональных решений. Эндрю Бремнер и Кассельс доказали верность этого утверждения для всех простых чисел соответствующего вида до 1000. Оказалось, что, даже если ранг известен и мал, найти решения, позволяющие получить почти все остальные, может быть очень трудно. Они выяснили, что для p = 877 простейшим решением такого рода является рациональное число
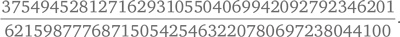
Доказано огромное число теорем, имеющих отношение к гипотезе Берча — Свиннертон-Дайера (обычно с очень серьезными формальными ограничениями), но это пока мало помогло в продвижении к полному решению этой задачи. В 1976 г. Коутс и Уайлс обнаружили первые указания на то, что эта гипотеза может быть верна. Они доказали, что один частный случай эллиптической кривой имеет ранг 0, если L-функция Дирихле не обращается в нуль в точке 1. Для такой эллиптической кривой число решений связанного с ней диофантова уравнения конечно, возможно, равно нулю, и определить это можно по соответствующей L-функции. После этого момента удалось сделать несколько технических шагов, по-прежнему ограниченных в основном рангами 0 и 1. В 1990 г. Виктор Колывагин доказал, что гипотеза Берча — Свиннертон-Дайера верна для рангов 0 и 1.
Более детальные гипотезы, требующие серьезной компьютерной поддержки, соотносят константу c в гипотезе Берча — Свиннертон-Дайера с различными концепциями теории чисел. Существуют аналогичные гипотезы — впрочем, столь же загадочные, — для алгебраических числовых полей. Известно также, что большинство (в точном смысле) эллиптических кривых имеет ранг 0 или 1. В 2010 г. Манджул Бхаргава и Арул Шанкар объявили, что им удалось доказать: средний ранг эллиптической кривой не превосходит 7/16. Если это доказательство и доказательство некоторых других недавно опубликованных теорем будут признаны математическим сообществом, то получится, что гипотеза Берча — Свиннертон-Дайера верна для ненулевой доли всех эллиптических кривых. Однако речь пока идет о простейших кривых, не представляющих, по существу, кривые более сложной структуры, ранга 2 и более. Они пока остаются для нас загадкой.
15. Комплексные циклы. Гипотеза Ходжа
Некоторые области математики вполне можно соотнести с тем, с чем мы встречаемся в повседневной жизни. Уравнение Навье — Стокса невозможно встретить на кухне, но мы все понимаем, что такое жидкости, и представляем, как они текут. Другие области можно соотнести с эзотерическими вопросами переднего края науки: так, чтобы разобраться в квантовой теории поля, нужна хотя бы докторская степень в области математической физики, но аналогии с электричеством и магнетизмом или такие хоть сколько-то представимые образы, как волны вероятности, позволяют кое-что понять. Третьи можно объяснить при помощи картинок, и хороший пример тому — гипотеза Пуанкаре. Но некоторые области математики не поддаются ни одному из перечисленных способов и никак не позволяют сделать сложные абстрактные понятия доступными.
Гипотеза Ходжа, сформулированная в 1950 г. шотландским геометром Уильямом Ходжем, — одна из таких задач. Проблемы здесь возникают не из-за доказательства, поскольку его просто нет. Все дело в утверждении. Вот так примерно эта задача сформулирована на сайте Института Клэя:
«На любом невырожденном проективном комплексном алгебраическом многообразии любой класс Ходжа представляет собой рациональную линейную комбинацию классов алгебраических циклов».
На первый взгляд в этой формулировке понятны, пожалуй, только предлоги и такие слова, как «любой». Остальное понятно, как отдельные слова: «многообразие», «класс», «рациональный», «цикл». Но образы, порождаемые этими словами, — виды в живой природе, школа, разум без эмоций, какой-то повторяющийся процесс — явно относятся не к тому, что имел в виду Институт Клэя. Остальное еще более очевидный жаргон. Но не просто жаргон ради жаргона — не сложные слова, за которыми прячется профессиональная лексика. Точнее, это простые слова для обозначения сложных вещей. В обычном языке нет готовых названий для подобных концепций, так что часть приходится заимствовать в других областях, а часть изобретать заново.
Если говорить о хорошем, то здесь у нас появляются немалые возможности. Можно сказать, что гипотеза Ходжа лучше представляет реальную математику XX и XXI вв., чем любая другая из рассмотренных в этой книге тем. Подойдя к ней надлежащим образом, мы сможем получить представление о том, насколько концептуально продвинута на самом деле современная передовая математика. В сравнении со школьной математикой она как Эверест в сравнении с кучкой земли, оставленной кротом.
Но, может быть, это всего лишь пустое сотрясание воздуха, претенциозная чепуха, которой занимаются отшельники в башнях из слоновой кости? Если ни один нормальный человек не в состоянии понять, о чем идет речь, зачем впустую переводить деньги налогоплательщиков на тех, кто думает о подобных вещах? Однако давайте взглянем на это с другой стороны. Предположим, любой человек мог бы понять все, о чем думают математики. Неужели тогда вы с удовольствием отдали бы математикам деньги налогоплательщиков? Разве им платят не за профессиональные знания? Если бы все было настолько просто и понятно, что разобраться в этом мог бы любой, зачем вообще надо было бы готовить математиков? А если бы каждый умел налаживать центральное отопление и сваривать трубы, для чего были бы нужны водопроводчики?
Я не могу сказать вам, как именно могла бы быть с пользой применена гипотеза Ходжа. Но я могу объяснить, насколько важное место она занимает в математике. Современная математика — единый организм, так что значительное продвижение в любой из основных областей со временем принесет вполне материальный доход, измеряемый в долларах и центах. Может быть, сегодня мы не найдем на своей кухне ни одного прибора, сделанного на основе этой гипотезы, но завтра — кто знает? Тесно связанные с ней математические концепции уже доказывают свою полезность в различных областях науки — от квантовой физики и теории струн до робототехники.
Иногда новые математические идеи получают практическое применение почти сразу. Иногда этот процесс занимает не одно столетие. Быть может, в последнем случае лучше было бы подождать, пока возникнет нужда в этих идеях, а затем ударными темпами провести их разработку? Быть может, все математические задачи, не имеющие немедленного и очевидного применения, следует откладывать в дальний ящик на будущее? Однако если бы мы так поступали, то всегда отставали бы от жизни, поскольку математики уже несколько сотен лет играют в догонялки с прикладной наукой. Да и не всегда можно точно сказать, какая идея необходима в данный момент. Как вы думаете, понравилось бы вам, если бы никто даже не задумался о производстве кирпичей, пока вы не пригласили бы рабочих для строительства дома? Чем оригинальнее математическая концепция, тем более маловероятно, что она родится в результате ударной разработки.

