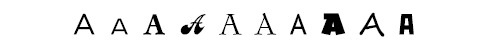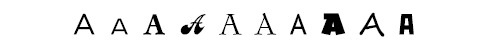
Когнитивист Дуглас Хофштадтер однажды сказал, что распознать букву А – настоящая проблема для искусственного интеллекта! Данное язвительное замечание, несомненно, является сильным преувеличением, но доля истины в нем есть: даже в таком тривиальном контексте люди умело справляются с абстракциями. Этот наш дар лежит в основе одного забавного явления повседневной жизни капчи – коротенькой последовательности букв, которую просят распознать некоторые сайты, дабы убедиться, что вы человек, а не машина. Многие годы капчи успешно противостояли машинам. Но компьютерная наука развивается быстро: в 2017 году искусственной системе удалось распознать капчу почти на человеческом уровне18. Неудивительно, что этот алгоритм имитирует человеческий мозг сразу в нескольких отношениях. Совершая истинный tour de force
[11], он умудряется извлечь скелет каждой буквы, внутреннюю сущность буквы А, после чего использует все ресурсы статистического мышления, чтобы проверить, применима ли эта абстрактная идея к имеющемуся образу. И все же этот компьютерный алгоритм, каким бы сложным он ни был, работает только с капчами. Наш мозг применяет способность распознавать абстракции во всех аспектах повседневной жизни.
Эффективная обработка данных. Все согласятся с тем, что современные нейронные сети обучаются слишком медленно: им требуются тысячи, миллионы, даже миллиарды элементов данных, чтобы сформировать представление об определенной области. У нас даже есть экспериментальные доказательства этой медлительности. Например, чтобы научиться приемлемо играть на консоли Atari, нейронной сети, разработанной DeepMind, необходимо минимум 900 часов, а человеку – всего 2!19 Другой пример – овладение речью. По оценкам психолингвиста Эммануэля Дюпу, в большинстве французских семей дети слышат от 500 до 1000 часов речи в год; этого более чем достаточно для усвоения языка Декарта, даже с такими мудреностями, как soixante douze («семьдесят два») или s'il vous plaît («пожалуйста»). С другой стороны, в племени цимане, населяющем север боливийской Амазонки, дети слышат только 60 часов речи в год, но это отнюдь не мешает им отлично говорить на языке цимане. Для сравнения: лучшие современные компьютерные системы от Apple, Baidu и Google требуют в 20–1000 раз больше данных, чтобы достичь даже мизерной языковой компетенции. В плане научения эффективность человеческого мозга остается непревзойденной: машины способны поглощать огромное количество информации, зато мы способны обрабатывать ее более эффективно. Иными словами, из минимума данных люди умеют извлекать максимум.
Социальное научение. Человек – единственный вид, который добровольно делится информацией: мы многому учимся у других людей благодаря речи. Данная способность до сих пор остается вне досягаемости современных искусственных нейросетей. В искусственных моделях знания зашифрованы, рассеяны в значениях сотен миллионов синаптических весов. В этой скрытой, имплицитной форме их нельзя извлечь и избирательно передать другим. Мы, напротив, можем эксплицитно сообщить другим информацию самого высокого уровня – ту, которая достигает нашего сознания. Сознательное знание неразрывно связано с возможностью его вербального выражения: всякий раз, когда мы приходим к более или менее четкому пониманию некоего явления, ментальная формула находит отклик в нашем языке мышления, и мы можем сообщить о ней окружающим с помощью речи. Необычайная эффективность, с которой человек делится своими знаниями с другими, используя минимальное количество слов («Чтобы попасть на рынок, поверните направо, на маленькую улочку за церковью»), до сих пор беспрецедентна как для животного мира, так и для мира компьютеров.
Научение с одной попытки. Ярчайший пример такой эффективности – усвоение нового материала с первой попытки. Если я употреблю новый глагол, скажем, «курдячить»
[12], хотя бы один раз, вы тоже сможете его использовать. Конечно, некоторые искусственные нейросети могут запомнить мою фразу. Но что машины пока не умеют делать хорошо, так это интегрировать новую информацию в существующую сеть знаний – а человеческому мозгу это отлично удается. Вы не только запоминаете новый глагол «курдячить», но и мгновенно понимаете, как его спрягать и вставлять в другие предложения: вы часто курдячите? я курдячил вчера, а они курдячат сегодня. Когда я говорю: «Давайте покурдячим завтра» – вы не просто узнаете новое слово, вы вставляете его в обширную систему символов и правил. Например, «курдячить» – личный глагол II спряжения (я курдячу, ты курдячишь, он курдячит и т.д.). Научиться – значит успешно внедрить новые знания в существующую сеть.
Систематичность и язык мышления. Грамматические правила – лишь один из примеров необычайного таланта нашего мозга: способности обнаруживать общие законы, лежащие в основе конкретных случаев. Будь то математика, язык, наука или музыка, человеческий мозг ухитряется извлекать из них абстрактные принципы, систематические правила, которые он может вновь применить в самых разных контекстах. Возьмем, к примеру, арифметику: наша способность складывать два числа носит очень общий характер – как только мы научились этой процедуре на малых числах, мы без труда можем применить ее к произвольно большим числам. Но главное – мы умеем делать обобщающие выводы. Многие дети в возрасте пяти-шести лет обнаруживают, что за каждым числом n следует число n + 1 и что последовательность целых чисел, следовательно, бесконечна – наибольшего числа просто не существует. Лично я до сих пор с трепетом вспоминаю момент, когда я это осознал – на самом деле, это была моя первая математическая теорема. Какие необыкновенные способности к абстракции! Каким образом нашему мозгу, состоящему из конечного числа нейронов, удается концептуализировать бесконечность?
Современным искусственным нейросетям недоступен даже такой простой абстрактный закон, как «за каждым числом следует другое число». Абсолютные истины – не их конек. Систематичность20, способность к обобщению на основе некоего символического правила, а не поверхностного сходства по-прежнему ускользает от большинства современных алгоритмов. Иронично, но так называемые алгоритмы глубокого обучения практически не приспособлены к глубокому анализу.
Наш мозг, напротив, превосходно умеет выводить формулы на своем собственном, ментальном языке. Например, он может выразить понятие бесконечного множества, ибо обладает внутренним языком, наделенным такими абстрактными функциями, как отрицание и квантификация (бесконечное = не конечное = за пределами любого числа). Американский философ Джерри Фодор (1935–2017) предложил теоретическое объяснение этой способности: он утверждал, что мы мыслим символами, которые комбинируются в соответствии с систематическими правилами особого «языка мышления»21. Возможности такого языка обусловлены его рекурсивной природой: каждый вновь созданный объект (скажем, понятие бесконечности) может быть немедленно использован в новых комбинациях, без ограничений. Сколько существует бесконечностей? Этот, казалось бы, абсурдный вопрос задал себе математик Георг Кантор (1845–1918) и сформулировал теорию трансфинитных чисел. Способность «бесконечно использовать конечный набор средств», согласно Вильгельму фон Гумбольдту (1767–1835), характеризует все человеческое мышление.