Когда игрок применяет оптимальную стратегию минимакс, он трансформирует развлекательную и непредсказуемую деятельность в механическое выполнение стратегических правил, которые приводят к определенному вероятностному распределению исходов. Представьте, что, играя в «Камень, ножницы, бумага», один из игроков применяет стратегию случайного выбора того, что показать. В таком сценарии каждый из трех возможных вариантов – камень, ножницы или бумага – может быть выбранным с вероятностью 33,3 %. Вне зависимости от стратегии оппонента это приведет исход игры к схеме нормального распределения, оставляя каждому игроку пятидесятипроцентный шанс на выигрыш. Можно сказать, что такой подход устранит игровой элемент.
Современная портфельная теория делает то же самое с торгами на финансовых рынках. Согласно Марковицу и Шарпу, рынок – это не игра, где игроки соревнуются, стараясь предсказать движения рынка. Современная портфельная теория трансформирует финансовые торги в механическое применение стратегических правил, которое распределяет прибыли базовой экономики среди инвесторов пропорционально их инвестициям в финансовый рынок. Таким образом, современная портфельная теория убирает игровой элемент из торгов на финансовых рынках.
Фантазии ценообразования
Принципиально важно вспомнить, что модель выбора портфеля, созданная Марковицем и усовершенствованная Шарпом, все равно опирается на вводные данные, необходимые для определения того, чтó должно быть включено в портфель; эти данные состоят из оценок доходности и дисперсии различных ценных бумаг, рассматриваемых для портфеля. Для этого нужен некий вариант фундаментального анализа. Марковиц замечает: «Чтобы использовать правило E – V при выборе ценных бумаг, нам необходимы процедуры для нахождения приемлемой μi ожидаемой доходности и σij ковариации. Эти процедуры, я полагаю, должны совмещать статистические техники и суждения практиков»
[94]. Такие «практики» – это фундаментальные аналитики.
То, что Марковиц предлагает – это просто-напросто количественный метод для решения проблемы диверсификации. В терминологии Башелье портфельная теория Марковица исследует математическую область априорных вероятностей. При этом теория Марковица все равно опирается на данные, образовавшиеся в области апостериорных вероятностей, то есть в области фундаментального анализа. У Башелье мы находим стремление к науке, полностью свободной от этой последней области. Башелье очевидно пренебрегает выводами, вытекающими из этой области, поскольку они представляются «сугубо личностными», а не математически обусловленными.
После прорывов, совершенных Марковицем и Шарпом в сфере портфельной теории, следующим шагом в эволюции современных финансов может считаться развитие теории ценообразования опционов Блэком, Шоулзом и Мёртоном. Эта теория представляет из себя кульминацию истории дисциплины финансов, поскольку она, похоже, осуществила мечту Башелье об исключительно количественной теории финансов, не замаранной регистром качественных суждений.
Теории Блэка, Шоулза и Мёртона относятся к производным финансовым инструментам. Деривативы – это финансовые продукты, которые не являются базовыми активами в производящей экономике. Они могут принимать разные формы, такие как опционы, фьючерсы, свопы и другие. Деривативы относятся только к ценам ценных бумаг, которые затем могут отсылать к чему-то за пределами рынка. В этом смысле рынки деривативов создают метарынки внутри финансовых рынков. Опцион на покупку акций, например, дает держателю право – но необязательно обязывает – купить определенное количество акций компаний по определенной цене в какой-то определенный момент в будущем. Деривативы любопытны тем, что они не отражают факт владения базовым активом, в том же виде, в каком акция отражает владение долей в компании. Это делает оценку деривативов очень замысловатым занятием.
На самом деле Башелье уже предложил формулу для ценообразования таких деривативов, как опцион на государственную облигацию. И хотя Блэк, Шоулз и Мёртон внесли некоторое количество корректировок и уточнений в изначальную модель Башелье, их основным достижением является, пожалуй, то, как они формализовали и обосновали свою модель, а не ее содержание как таковое, которое было опубликовано Блэком и Шоулзом в 1973 году. Блэк, Шоулз и Мёртон использовали эффективный рынок как мерило оценки верной цены опциона, что явилось новшеством. Эта идея описана в самом первом предложении важнейшей статьи Блэка и Шоулза: «Если опционы корректно оценены на рынке, то будет невозможно извлечь гарантированные прибыли за счет создания портфелей, состоящих из длинных и коротких позиций в опционах и их базовых акциях»
[95].
В данном случае Блэк и Шоулз прямо исходили из утверждения Башелье о том, что математическое ожидание спекулянта равно нулю. Когда эта аксиома применяется к рынкам деривативов, это означает, что на эффективном рынке невозможно получить прибыль путем арбитража между рынком деривативов и рынком базовых активов. Идея о невозможности арбитража развивается и у Мёртона
[96].
Опционы предоставляют их держателю возможность получать прибыль от роста цены базовой акции (или другого актива); держатель же рискует только тем, что заплатил за опцион, – в случае если цена акции остается постоянной или снижается. Поэтому мы можем себе представить ситуацию, когда трейдер приобретает опцион на покупку акций и одновременно в короткую продает определенное количество базовых акций. Если цена акции растет, он делает на опционе деньги, но теряет на короткой позиции. Если цена акции падает, он теряет то, что заплатил за опцион, но зарабатывает на короткой позиции. На эффективном рынке – так гласит аксиома теории Блэка, Шоулза и Мёртона – прибыль от такой стратегии нулевая вне зависимости от изменений цен акций, поскольку цена на опцион будет образована таким образом, что две части сделки станут друг друга аннулировать. Арбитраж невозможен.
Формула для «рационального» или «справедливого» расчета цены опциона может быть выведена из аксиомы о невозможности арбитража. Цена опциона должна отражать вероятность заработать на портфеле базовых акций, который воспроизводит опцион. Если вероятность сделать деньги высока, цена соответствующего опциона должна быть высокой. Если вероятность низка, цена должна быть низкой.
Формула Блэка и Шоулза для расчета европейского опциона колл выглядит так (разница между европейскими и американскими опционами колл будет объяснена позже):
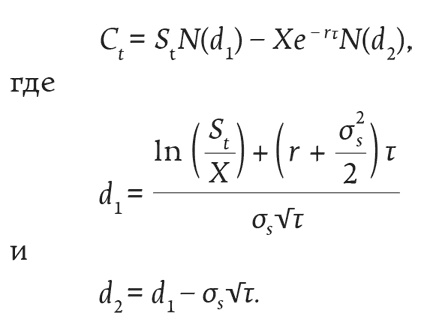
N(.) является всего лишь функцией кумулятивной плотности нормального распределения, так что цена опциона (С) есть функция пяти переменных: