Вероятность как символизация
Познавательная ценность теории вероятностей обусловлена тем, что массовые случайные явления в своем совокупном действии создают строгие, неслучайные закономерности
[87].
Используя философские термины, можно сказать, что Колмогоров описывает здесь трансформацию обычно хаотичного и непредсказуемого реального в упорядоченный и предсказуемый символический порядок с помощью теории вероятностей. Это то, что происходит при «вероятностном повороте» современных финансов, начатом Башелье и завершенном Марковицем и Шарпом. Для того чтобы объяснить, как теория вероятностей работает в категориях жижековской триады реальное – символическое – воображаемое, будет полезным задействовать конкретный пример преобразования реального в символическое, который предоставляет Лакан.
Игра с подбрасыванием монетки часто используется в финансовой теории для того, чтобы проиллюстрировать, как случайность и вероятность работают на финансовых рынках. А вот как Лакан использует эту игру, чтобы показать взаимодействие между реальным и символическим
[88]. Представьте следующее: подкидывая монетку десять раз, мы получим случайную последовательность выпадения орла или решки. Результат может выглядеть так:
Таблица 1 Последовательность подбрасываний

Сначала последовательность представляется в чистом виде хаотичным, беспорядочным и бессмысленным выражением реального. Теперь мы объединим отдельные подбрасывания в накладывающиеся друг на друга группы по три, то есть номера (1,2,3), (2,3,4), (3,4,5) и так далее. Эти совокупности обозначаются в соответствии со следующим правилом: (ООО, РРР) = (α); (ОРР, РОО, РРО, ООР) = (β); (ОРО, РОР) = (γ). Таким образом создается новая последовательность:
Таблица 2 Последовательность символизации
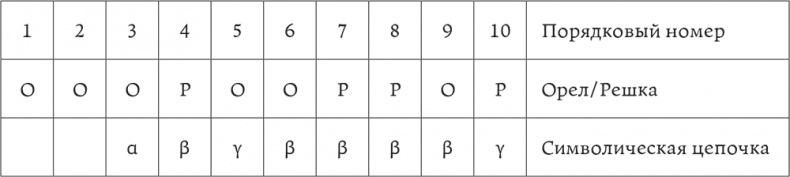
Хотя исходы в последовательности отдельных подбрасываний, разумеется, остаются совершенно случайными, символизация внесла элемент закономерности и упорядоченности в символическую цепочку. Определенные последовательности стали невозможными, а другие необходимыми. Например, γ не может следовать сразу за α, поскольку это бы означало сдвиг в ряду подбрасываний с орлов на решки, или наоборот. Такой сдвиг создал бы совокупность β между двумя другими. Еще одним примером является тот факт, что между двумя γ-совокупностями непременно должно быть четное число β-совокупностей. β символизирует сдвиг в последовательности с орлов на решки, или наоборот. Если бы подряд следовало три орла, должно было быть 0, 2, 4, 6 и т. д. таких сдвигов, прежде чем мы вернулись бы к трем последовательным орлам.
Лакан стремится показать, как упорядоченность и закономерность возникают ex nihilo из символизирования чистой случайности реального, хотя поначалу символизация может показаться «невинной» процедурой фиксирования реальных событий. Это сопоставимо с привнесением порядка в хаос через процедуры символизирования и агрегирования теории вероятностей. Лакан обобщает суть игры с монеткой замечанием, чрезвычайно похожим на приведенную выше цитату из Колмогорова: «Мы наблюдаем выделенную из реального символическую закономерность, которая исправно фиксирует любую непроизвольность реального, но тем самым еще больше подчеркивает его произвольность»
[89].
У Марковица мы обнаруживаем две такие процедуры для агрегирования. Первая – обращение с неопределенностью будущей траектории движения ценной бумаги как с риском смещает фокус с сиюминутных движений цены вверх/вниз на долгосрочную перспективу. Это позволяет тому, кто принимает финансовые решения, игнорировать краткосрочные колебания и основывать свою торговую стратегию на расчете вероятностей. Вторая заключается в переходе от выбора отдельных акций к созданию портфеля, что тоже всегда позволяет рассматривать ценные бумаги в совокупности. И вновь торговая стратегия основывается не на предсказании поведения отдельных ценных бумаг, а на расчете вероятности поведения совокупности ценных бумаг в портфеле. Иными словами, расчет вероятностей представляет из себя процедуру символизирования реального, в результате чего становится возможным принимать рациональные решения перед лицом обычно непредсказуемых событий. В рамках такого управления риском мы наблюдаем то, что Хакинг называл укрощением случайности
[90].
Фантазия о присоединении к рынку
Важно отметить, что в случае теории вероятностей утверждение Жижека о том, что символизация не является полной, остается верным. Закон больших чисел является законом именно о больших, а не о малых числах. Только на совокупном уровне последовательность событий представляет принцип упорядоченности. Только на совокупном уровне случайность укрощается. Отдельное событие остается беспорядочным, неукрощенным и «не поддающимся законам». Историк Томас М. Кавана суммирует недостатки теории вероятностей:
Теория вероятностей дает ответ на случайность, создает отдельное научное направление. Однако она может сделать это, только отказавшись сперва от любых притязаний говорить о том, что с точки зрения игрока, человека, ожидающего исход случайного события, является самым важным: о текущем моменте, о том, что дальше произойдет, о конкретном событии. Как наука о случайности теория вероятностей может говорить о реальном, но для этого ей сначала нужно выйти за пределы реального, заняв выгодную отстраненную позицию, исключающую какое бы то ни было вовлечение в один, а не другой исход. Та реальность, о которой говорит теория вероятностей, всегда абстрактна и не имеет сколько-нибудь убедительного отношения к какому бы то ни было конкретному моменту или ситуации
[91].
Таким образом, отдельное событие является избытком реального, который выпадает из символизации. Отдельное событие обозначает границу теории вероятностей. Идея здесь такая же, что и у Башелье. Современная финансовая теория мало что может сказать о движении вверх/вниз цены одной акции или другой ценной бумаги в самом ближайшем будущем. Поэтому непосредственное движение цены вверх/вниз является избытком реального, который «сопротивляется символизации».




