Раздел 11 — показательные функции и уравнения
• Я могу показать, что показательная функция имеет один и тот же множитель при равных интервалах изменения переменной.
• Я могу указать случаи, когда изменение скорости описывается одним и тем же множителем за равные промежутки времени и которые могут быть описаны с помощью показательных функций.
• Я могу использовать графики или таблицы, чтобы сравнить скорость изменения линейной, квадратичной и показательной функций.
• Я могу преобразовать показательную функцию, используя ее свойства.
• Я могу использовать параметры показательной функции, взятые из реальной жизни.
• Я могу построить график показательной функции, определив ее основные характеристики: отрезки, отсекаемые на координатных осях, максимальное и (или) минимальное значения, асимптоты и поведение функции на границах области ее определения.
• Я могу построить диаграмму рассеяния, используя показательную функцию в методе наилучшего приближения, и применить ее для составления прогнозов.
Источник: предоставлено Лизой Хенри.
Две звезды и пожелание

Размышления

Над какой интересной концепцией мы работали сегодня?
Что я узнал сегодня?
Какие хорошие идеи появились у меня сегодня?
В каких ситуациях я мог бы использовать полученные сегодня знания?
Какие вопросы у меня есть по поводу сегодняшней работы?
Какие новые идеи появились у меня под влиянием этого урока?
Мозаичная задача А по алгебре
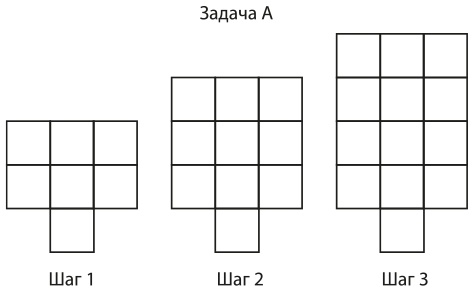
Мозаичная задача Б по алгебре
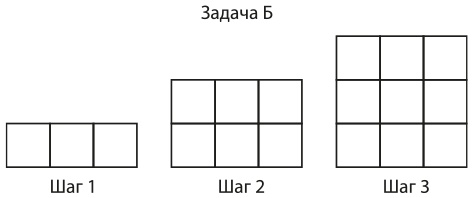
Мозаичная задача В по алгебре
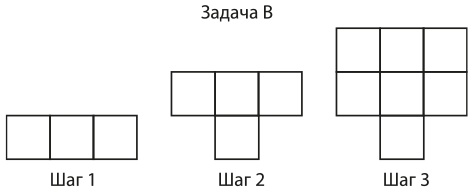
Мозаичная задача Г по алгебре
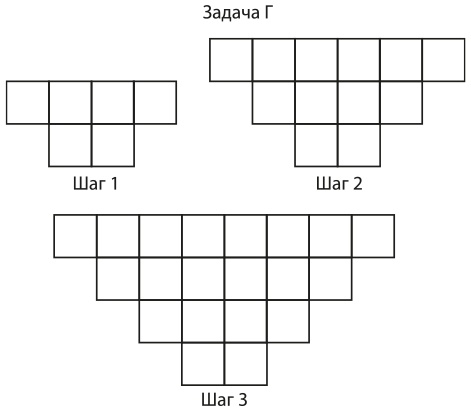
Билет на выход
Билет на выход _____ Имя _____ Дата _____

Талон на выход _____ Имя _____ Дата _____

Самооценка «Покажите, что вы можете сделать»
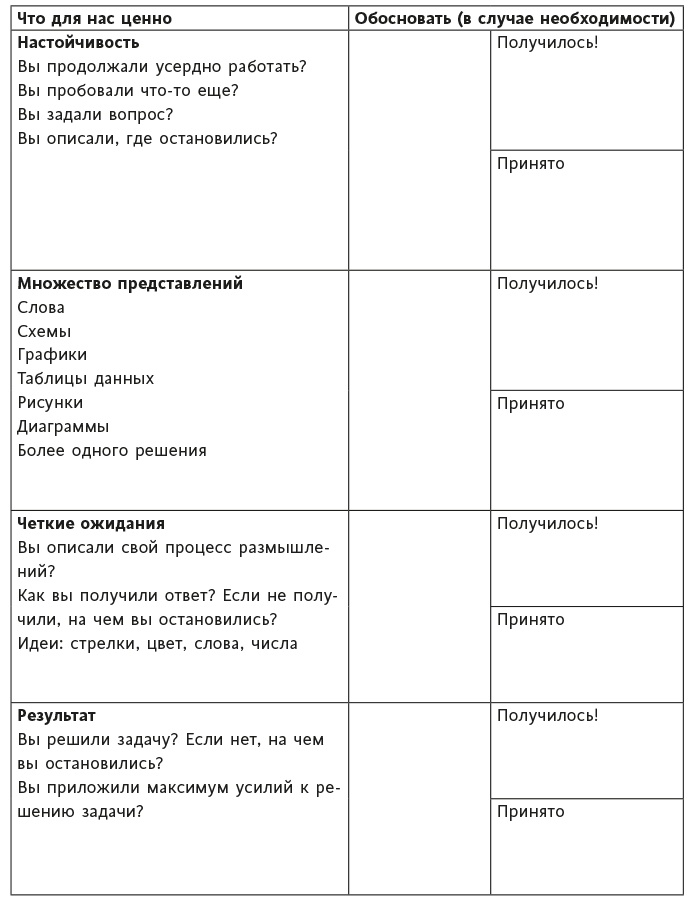
Источник: предоставлено Эллен Круз.
Математические цели оценки участия в работе группы
Ваша группа добьется успеха сегодня, если вы будете:
• понимать и описывать закономерности;
• обосновывать ход своих мыслей и применять разные способы представления;
• устанавливать связи между разными подходами и представлениями;
• использовать слова, стрелки, числа и цветовое кодирование для четкого разъяснения идей;
• ставить вопросы, чтобы понять ход мыслей других членов команды;
• ставить вопросы, чтобы подтолкнуть группу к более глубокому анализу;
• готовить презентацию, чтобы ученики, не входящие в состав вашей группы, могли понять ход ее мыслей.
Никто не может успешно применять все эти методы работы, но каждый способен овладеть некоторыми из них. Необходимо, чтобы все члены вашей группы справились с сегодняшним заданием.
Источник: материал предоставил Карлос Кабана.
Групповые цели оценки участия в работе группы
Во время теста на оценку участия в работе группы я буду наблюдать, как вы:
• склоняетесь над столом и работаете;
• поровну делите время для высказываний;
• поддерживаете друг друга;
• слушаете друг друга;
• задаете друг другу много вопросов;
• отрабатываете свои роли в группе.
Источник: материал предоставил Карлос Кабана.
Собачьи галеты
Сколько существует способов разделить 24 собачьи галеты на две группы?
Сколько существует способов разделить 24 собачьи галеты на равные группы?
Представьте полученный результат в графическом виде, отобразив все комбинации.
Акцент на математических связях
Изобразите дроби 3/4, 6/8 и 12/16 графически.
Представьте эти дроби в виде подобных треугольников.
Чем схожи и чем отличаются эти формы представления дробей — графическая; в виде чисел; в виде треугольников? Можете ли вы применить цветовое кодирование к различным свойствам каждой формы представления, чтобы эти свойства были показаны одним цветом в разных представлениях?
Цветовое кодирование шоколадного пирога
Сэм испек шоколадный пирог, который собирается разрезать на 24 равные части. Он хочет разделить его поровну с 5 своими друзьями. Разделите пирог на части и воспользуйтесь методом цветового кодирования, чтобы показать, сколько кусочков пирога получат Сэм и его друзья.
Раскрашенный куб
Представьте себе куб 5 × 5 × 5, внешние грани которого раскрашены в один цвет, причем этот куб состоит из меньших кубиков размером 1 × 1 × 1.
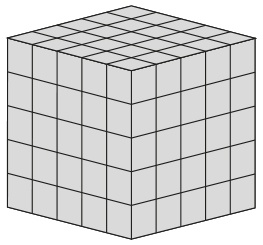
Дайте ответы на следующие вопросы.
У скольких маленьких кубиков будет 3 раскрашенные грани?
У скольких маленьких кубиков будет 2 раскрашенные грани?












