Члены группы:
Дата:
Мы хотели бы знать: __________
Используйте рисунки, числа и слова, чтобы показать, как вы ответили на этот вопрос.
Мы хотели бы проанализировать: __________
Используйте рисунки, числа и слова, чтобы показать, как вы ответили на этот вопрос.
Ученики с воодушевлением начали размышлять над такими вопросами: почему готовые браслеты обходятся так дорого? Они смогли найти ответ, выяснив, во сколько обошлось бы самостоятельное изготовление браслетов, а затем проанализировав затраты на продажи через магазин. Ученики задавали реальные вопросы, которые требовали большей вовлеченности и обучения.
После выхода на рынок труда в нашем высокотехнологичном мире от учеников будут ожидать выполнения одной очень важной работы: постановки вопросов в связи с различными ситуациями или большими объемами данных. Компаниям все чаще приходится иметь дело с огромными массивами данных, поэтому сотрудников, которые умеют задавать творческие и интересные вопросы, будут высоко ценить на работе. Когда я предлагала ученикам рассмотреть ту или иную ситуацию и сформулировать свои вопросы, они сразу включались в работу, с воодушевлением опираясь на собственные идеи. Такой метод легко реализовать на уроках математики, и его необходимо время от времени использовать. Люди должны иметь возможность освоить его в школе, чтобы быть готовыми к его применению в дальнейшей жизни.
Рассказывая о своей роли в качестве работодателя, Конрад Вольфрам говорит, что ему не нужны сотрудники, которые умеют быстро считать, поскольку это могут делать компьютеры. Ему нужны сотрудники, способные выдвигать гипотезы и говорить о своих математических методах. Крайне важно, чтобы сотрудники рассказывали о своих математических методах другим членам команды: тогда остальные также смогут воспользоваться этими методами в своей работе и исследованиях и смогут увидеть, есть ли ошибки в соответствующих размышлениях или логике. В этом и состоит суть математической работы, которая называется рассуждением.
Я беседую о стандартах Common Core по математике со многими родителями, и мне часто задают такой вопрос (особенно родители сильных учеников): «Зачем моему ребенку обсуждать свою работу в группе, если он может сам получить все ответы?» Я говорю таким родителям, что объяснение своей работы — практика, которая называется логическим рассуждением и лежит в основе математики. Когда ученики выдвигают доводы в пользу своих идей и обосновывают свой ход мыслей, они занимаются истинной математикой. Ученые предлагают теории и ищут примеры, которые доказывают или опровергают эту теорию. Математики предлагают теории и рассуждают о своих математических методах, обосновывая установленные ими логические связи между этими идеями (Boaler, 2013c).
В главе 5 шла речь об учебной стратегии, в соответствии с которой ученикам предлагают быть скептиками, побуждая друг друга к высокому уровню рассуждений. Это превосходный способ научить учеников рассуждать и брать на себя роль скептиков, что им очень нравится. Как было сказано в главе 5, рассуждение — не только важнейшая математическая практика, но и учебная, которая обеспечивает равенство, предоставляя всем доступ к идеям. Выступая в роли скептиков, ученики получают возможность задавать вопросы другим; при этом им не приходится брать на себя роль того, кто ничего не понимает.
Используйте современные технологии и развивающие материалы
Показывая ученикам мир открытой, визуальной и творческой математики, целесообразно использовать разные элементы современных технологий и развивающие материалы. Счетные палочки Кюизенера, соединяющиеся кубики и занимательная мозаика помогают учащимся на всех уровнях; я использую их даже в работе со студентами Стэнфорда. В главе 4 представлен анализ приложений и игр, которые также развивают концептуальное и визуальное мышление. В главе 4 я сфокусировалась на числах, но есть много хороших приложений, позволяющих ученикам исследовать геометрические идеи в двух или трех измерениях, перемещая углы и прямые, чтобы изучить соотношения. Это важные и эффективные размышления, которые невозможно выполнить с помощью ручки и бумаги. Приложения Geometry Pad для iPad и GeoGebra позволяют учителям и ученикам создавать свои динамичные изображения и исследовать геометрические и алгебраические понятия, такие как y = mb + x, и тригонометрические функции в режиме динамического визуального отображения. Приложение Geometry Pad выпускает компания Bytes Arithmetic; его базовая версия есть в бесплатном доступе.
Другие приложения, например Tap Tap Blocks, помогают ученикам строить объекты в трех измерениях, создавая и решая пространственные и алгебраические закономерности (см. рис. 9.12). Ученики могут размещать и вращать объекты в искусственно созданном трехмерном пространстве. Tap Tap Blocks — бесплатное приложение, работающее на базе iOS, которое разработал Пол Хангас.
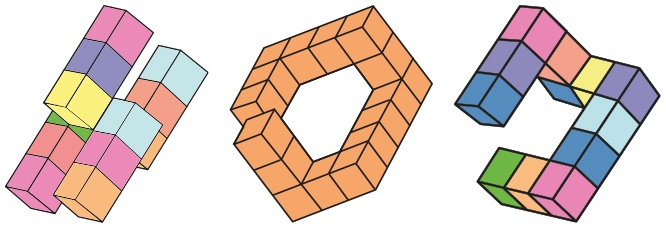
Рис. 9.12. Tap Tap Blocks
С помощью приложения можно предложить ученикам выполнить такое задание: создать фигуру, сделать несколько ее скриншотов с разных сторон, а затем предложить одному из друзей составить свою фигуру (см. рис. 9.13).
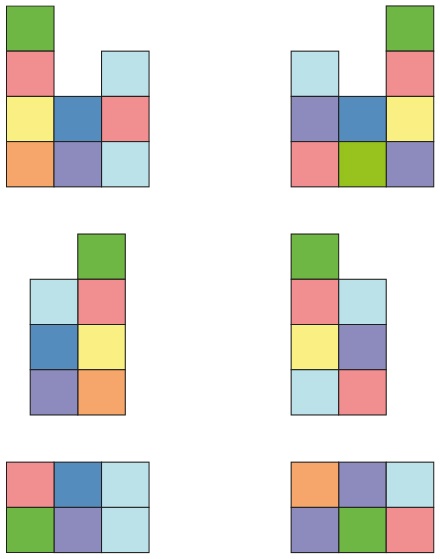
Рис. 9.13. Вид фигуры, созданной в приложении Tap Tap Blocks, с шести разных сторон
Можешь ли ты построить свою фигуру, в которой 1 оранжевый, 1 желтый, 1 синий, 2 зеленых, 2 голубых, 2 красных и 3 фиолетовых блока? Вот несколько скриншотов этой фигуры с разных сторон.
Все эти программы предлагают эффективный способ вовлечения учеников в процесс концептуального и визуального мышления, но есть и другие приложения, игры и сайты, обеспечивающие такую возможность. Существует множество приложений и игр, которые якобы могут помочь ученикам, но немногие из них опираются на результаты исследований по теме обучения, чтобы представить математику как концептуальную и визуальную дисциплину. Я рекомендую избирательно подходить к выбору технологий для работы с учениками и использовать только то, что стимулирует их размышлять и выдвигать гипотезы, а не развивать скорость выполнения процедур и вычислений.
Математика — широкая, многоплановая дисциплина, и когда учителя будут учитывать ее многоплановость при преподавании и оценке знаний, гораздо больше учеников получат доступ к математике и испытают воодушевление в связи с этим. Открывая математику, мы увеличиваем число и расширяем круг учеников, которые смогут успешно заниматься этой дисциплиной. Это не искусственное расширение или упрощение; это скорее такое расширение, которое приближает школьную математику к истинной и к математике реального мира.




