Предлагая ученикам взять задачу из реального мира, основанную на реальных данных и ограничениях, и решить ее с помощью математики, мы тем самым предлагаем им смоделировать соответствующую ситуацию. По словам Вольфрама, ученики должны столкнуться с задачей реального мира или найти ее, составить модель решения, выполнить вычисления (возможно, с помощью калькулятора или компьютера), а затем выяснить, верен ли полученный ответ или модель необходимо усовершенствовать. Он обращает внимание на то, что сейчас ученики тратят 80% времени на уроках математики на выполнение вычислений, а вместо этого им следует работать над тремя другими аспектами: созданием моделей, их уточнением и использованием для решения реальных задач.
На уроках алгебры ученикам часто предлагают вычислить что-то, а не создать модель с использованием алгебры. Возьмем в качестве примера такую задачу.
Человек, который придерживается диеты, идет в магазин, чтобы купить индюшатины. Ему дают три кусочка, общий вес которых составляет 1/3 фунта, но в диете сказано, что он может съесть только 1/4 фунта. Какую часть купленного мяса может съесть этот человек, чтобы не нарушить диету?
Для многих это трудная задача. Но проблемы, с которыми сталкивается большинство, связаны не с вычислениями, а с созданием модели решения. Я много где писала об элегантных визуальных решениях, которые нашли дети для этой задачи (Boaler, 2015a). Вот то, которое предложил один ученик четвертого класса.
Если три кусочка весят 1/3 фунта, то один фунт можно представить в виде 9 кусочков, как показано на рис. 9.9.

Рис. 9.9. Девять кусочков
Если он может съесть четверть фунта, то это количество, отображенное в одном квадранте на рис. 9.10, что составляет 21/4 кусочка.
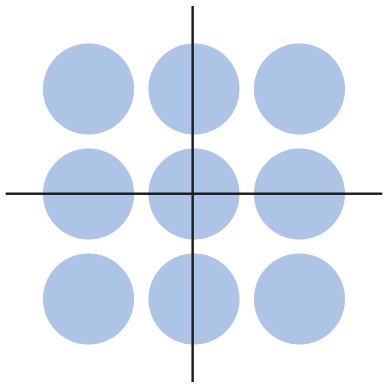
Рис. 9.10. Девять кусочков, разделенных на квадранты
Взрослые же изо всех сил старались решить задачу традиционными методами: они либо неправильно умножали, либо пытались применить алгебру, но не помнили, как именно это делать. Чтобы использовать алгебру, им нужно было сказать:
…а затем применить метод перекрестного умножения и получить x = 9/4.
У взрослых, которым ставили эту задачу, возникали трудности с созданием модели и составлением выражения. На уроках алгебры дети почти не получают опыта интерпретации ситуаций и создания моделей. Их учат перемещать переменные на странице и решать множество примеров, но они редко занимаются постановкой задач, а это и есть важный аспект того, о чем говорит Вольфрам: создания модели.
Моделированием могут заниматься люди всех возрастов. Например, ученикам подготовительного класса начальной школы можно предложить составить схему размещения детей в классе, чтобы все они могли поместиться на ковре. Ученики могут представить каждого ребенка в виде какой-нибудь фигуры и найти подходящий способ их размещения на ковре. Это пример моделирования ситуации, в данном случае с помощью фигур или предметов, символизирующих более сложные объекты (маленьких детей!): YouCubed at Stanford University, 2015b; www.youcubed.org/task/moving-colors.
Математические модели часто отличаются большей простотой по сравнению с реальными ситуациями. В примере с подготовительным классом фигуры, символизирующие детей, не учитывают их размер или движения. В примере с кусочками индюшки подразумевается, что все они имеют одинаковый размер и вес и между ними нет никаких различий.
Эта задача помещена в нереальный контекст, но он позволяет ученикам проанализировать разные аспекты реальной ситуации и использовать их в своих размышлениях. Вероятно, ученики захотят определить площадь участка, по которому должен ходить козлик. Либо сами ученики, либо учитель может предложить оградить участок забором. Отличное расширение этой задачи состоит в том, чтобы предложить ученикам определить, как они разместят 60 планок шириной 30 см, чтобы максимально увеличить дополнительную площадь. Это замечательная, содержательная задача, о которой шла речь в главе 5. Размышляя о посадке дерева, ученики могут задать себе вопрос: что будет, если козлик съест саженец? Какое дерево лучше всего посадить? Где его лучше посадить, чтобы козлик его не съел, но мог быть в тени?
Хорошая задача на моделирование, над которой могут работать ученики средних и старших классов, — известная задача о привязанном козлике. Ее расширенный вариант, представленный в примере 9.8, составила Кэти Уильямс.
ПРИМЕР 9.8. ПРИВЯЗАННЫЙ КОЗЛИК
Представьте себе козлика, привязанного веревкой в углу затененного участка площадью 1 × 2 м. Длина веревки равна 2 м.
Что еще нужно знать об этой ситуации?
Представьте эту ситуацию в виде рисунка.
Какие вопросы у вас возникли?
Солнце восходит на востоке затененного участка и садится на западе. Козлик хотел бы оставаться в тени. Где лучше посадить дерево? Какое дерево вы посадили бы?
В этой ситуации есть много возможностей для того, чтобы ученики задавали содержательные вопросы и искали на них ответы. Им понадобилось бы смоделировать эту ситуацию и представить ее в разных формах, то есть применить два важных математических подхода (рис. 9.11).
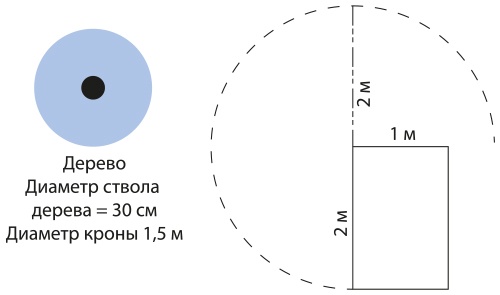
Рис. 9.11. Модель ситуации с привязанным козликом
Один из замечательных способов использовать реальные данные — предложить ученикам поработать с реальными числами и данными из журналов, газет и интернета. Например, мне очень нравится знакомить детей с вопросами социальной справедливости, предлагая им сформировать в классе группы, соответствующие разным континентам. Затем ученики анализируют, сколько печенья получит их группа, если оно символизирует долю мирового богатства, которая приходится на их континент (пример 9.9). Работая над этой задачей, ученики будут создавать модели, рассуждать и применять знания, а также изучать реальную и важную информацию об этом мире и о способах распределения богатства, что для них особенно актуально в пересчете на печенье, которое они смогут съесть. Поскольку ученики в некоторых частях мира получают совсем мало печенья, лучше сделать запас, чтобы выравнять потребление в будущем!
ПРИМЕР 9.9. МОДЕЛИРОВАНИЕ РАСПРЕДЕЛЕНИЯ МИРОВОГО БОГАТСТВА





