ПРИМЕР 9.5. АКЦЕНТ НА МАТЕМАТИЧЕСКИХ СВЯЗЯХ
Представьте дроби 3/4, 6/8 и 12/16 в виде графиков.
Представьте эти дроби в виде подобных треугольников.
Чем схожи и отличаются эти формы представления дробей — в виде чисел, графика и треугольников? Можете ли вы применить цветовое кодирование к различным свойствам каждой формы представления, чтобы эти свойства были представлены одним цветом в разных представлениях?
Обучайте учеников творческому и визуальному подходу к математике
На своих уроках я стимулирую творческий подход, ставя интересные задачи и придавая большое значение мыслительному процессу. Я говорю, что меня не интересует быстрота выполнения; мне нужно интересное представление идей, творческий метод или решение. Когда я использую такой подход к постановке математических задач, ученики всегда удивляют меня своим творческим мышлением.
Очень важно добиться того, чтобы ученики применяли визуальное мышление в процессе решения задач по математике. Это обеспечивает доступ к пониманию и задействованию разных путей в головном мозге. Аманда Кунлаба — учительница четвертого класса, которая объединяет искусство с основными школьными предметами, в том числе математикой. Она рассказывает, как однажды спросила своих учеников, элементы каких уроков искусства им больше всего понравились в основных школьных предметах. Она вспоминает, как один ученик «спокойно, но с воодушевлением объяснил, что ему нравится изобразительное искусство, поскольку творчество помогает ему “забыть о плохом”, и что ему это необходимо “чаще одного раза в неделю”» (Koonlaba, 2015).
Искусство и визуальное представление играют не только терапевтическую и творческую роль, хотя это очень важно. Они играют также решающую роль в обеспечении доступа к пониманию разных предметов. Когда я предлагаю детям визуализировать идеи и представить их в графическом виде, это всегда приводит к повышению уровня вовлеченности и созданию новых возможностей понимания математических концепций. Некоторым ученикам визуальное представление дается с трудом, но именно им использование этого подхода приносит самую большую пользу.
Кроме того, учителя должны постоянно предлагать ученикам связывать идеи, представленные в визуальной форме, с числовыми или алгебраическими методами и решениями. Как показано в главе 5, цветовое кодирование — хороший способ стимулировать установление таких связей. В следующих двух примерах мы видим, насколько цветовое кодирование может улучшить понимание учениками таких концепций, как геометрические фигуры, дроби и деление. В предыдущих главах приведены примеры применения цветового кодирования для алгебраических выражений и параллельных прямых. Когда ученики осваивают соотношения углов, им можно предложить раскрасить разные углы треугольника, разрезать рисунок и выстроить углы в линию, чтобы увидеть соотношения между ними. Визуальное представление углов поможет запомнить эти соотношения.
Понимание дробей тоже можно улучшить, предложив ученикам представить их с помощью цветового кодирования (см. пример 9.6 и рис. 9.5).
ПРИМЕР 9.6. ЦВЕТОВОЕ КОДИРОВАНИЕ ШОКОЛАДНОГО ПИРОГА
Сэм испек шоколадный пирог, который хочет разрезать на 24 равные части. Он намерен разделить пирог поровну со своими пятью друзьями. Разделите пирог на части и воспользуйтесь методом цветового кодирования, чтобы показать, сколько кусочков пирога получат Сэм и его друзья.
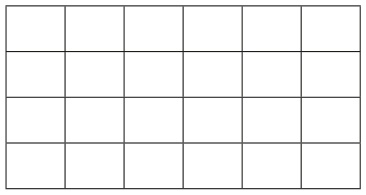
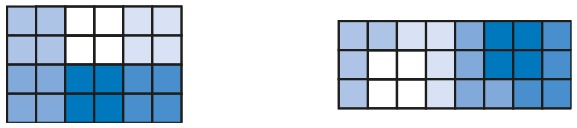
Рис. 9.5. Решение задачи с пирогом Сэма (пример 9.6)
Мне особенно нравится подход к цветовому кодированию деления, который разработали Тина Лаптон, Сара Пратт и Керри Ричардсон. Он состоит в том, чтобы предлагать всем ученикам решать задачи на деление с помощью «лоскутного одеяла», которое действительно помогает представить себе и понять разделение чисел на равные группы и остатки (рис. 9.6). Более подробное описание способов организации этого полезного вида деятельности см.: Lupton, Pratt, & Richardson, 2014.
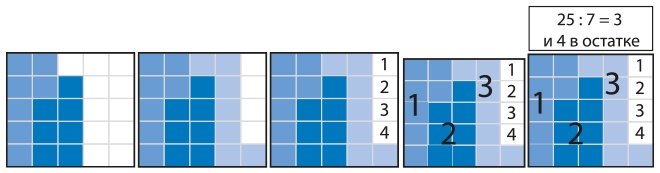
Рис. 9.6. Лоскутные одеяла деления
Источник: Lupton, Pratt, & Richardson, 2014.
Представление математических концепций разными способами — важная математическая практика, которую применяют специалисты по решению задач высокого уровня. Математики используют разные способы представления концепций — графики, таблицы, текстовое описание, выражения, а также (реже) рисунки и наброски. Мариам Мирзахани так описывает процесс размышлений над сложной математической задачей.
Не нужно записывать все детали… Но процесс рисования как-то помогает представить себе картину происходящего.
Мариам сказала, что ее трехлетняя дочь Анахита часто восклицает: «О, мамочка снова рисует!» — когда видит свою маму-математика за работой. «Может, она думает, что я художник?» (Klarreich, 2014).
Каждый раз, когда мне приходится решать сложную математическую задачу, я рисую ее; это лучший из известных мне способов решить трудную задачу и понять концепции, лежащие в ее основе. Работая с учениками, я предлагаю им представить задачу в графическом виде, когда у них возникают трудности; при этом я задаю им вопрос: «Вы пробовали нарисовать эту задачу?» Ученикам, которые не привыкли рисовать задачи, поначалу трудно, но они могут освоить этот метод, и он будет приносить им пользу. В главе 5 представлено больше идей по поводу способов, позволяющих увлечь учеников представлением математических задач в виде рисунков.
Поощряйте интуицию и свободу мысли
В главе 5 идет речь о том, как пользователи математики высокого уровня (такие, как Себастьян Трун, создающий роботы для Смитсоновского института) применяют интуицию для развития математических идей. Леоне Бертон провела интервью с 70 математиками-исследователями, чтобы определить характер их работы; 58 из них говорили о важной роли интуиции в этой работе. В книге «Что же такое математика?» Рубен Херш говорит о том, что «интуиция в математике повсюду» (Hersh, 1999).
Но что такое интуиция? И почему математики полагаются на нее, а ученики почти никогда не делают этого на уроках? Учителя могут стимулировать учеников к применению интуиции при решении любой математической задачи, предложив им подумать, как можно найти ответ, прежде чем объяснять им соответствующий метод. Возможности для интуитивного мышления можно использовать на всех уровнях изучения математики. Учителя начальной школы могут еще до объяснения материала предложить ученикам найти свой метод решения задачи. Например, спросить, как найти площадь коврика, до того как давать формулу площади. В средних или старших классах можно спросить учеников, как вычислить высоту объектов, которые слишком высоки, чтобы просто измерить их, прежде чем объяснять возможные методы решения этой задачи (Boaler, Meyer, Selling, & Sun, б/д). В главе 1 шла речь об уроке по началам анализа, на котором ученикам еще до объяснения теории предложили выдвинуть предположение и интуитивно поразмышлять над поиском объема лимона. И чтобы применить этот прием, не нужно почти ничего менять в методе преподавания.





