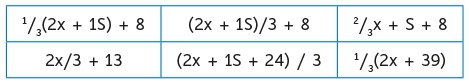1. Вместо того чтобы предлагать ученикам найти ответ на вопрос, чему равно 1/2 разделить на 1/4, предложите им предположить, сколько будет 1/2 разделить на 1/4, и придать ответу смысл, в том числе с помощью визуального представления решения. Как было сказано в главе 5, когда Кэти Хамфриз предложила ученикам решить задачу «1 разделить на 2/3», она начала с таких слов: «Вероятно, вы знаете правило, с помощью которого можно решить эту задачу, но сегодня оно не имеет значения. Я хочу, чтобы вы объяснили, почему ваше решение имеет смысл».
2. Вместо того чтобы предлагать ученикам упростить выражение 1/3(2x + 15) + 8 (типичная задача, которую ставят на уроках алгебры), предложите им найти все эквивалентные способы представления этого выражения. На рисунке 9.2 приведены примеры ответов.
3. Вместо того чтобы спрашивать учеников, сколько квадратов будет на шаге 100, спросите их, как они представляют себе рост закономерности, и предложите им использовать это понимание для обобщения закономерности до шага 100 (рис. 9.1).
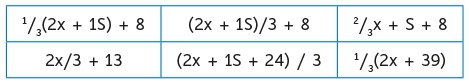
Рис. 9.1. Примеры алгебраических выражений
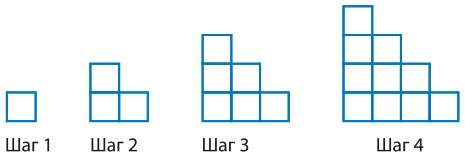
Рис. 9.2. Ступеньки
Любую математическую задачу можно открыть так, чтобы она обеспечивала ученикам больше пространства для обучения (подробнее см. главу 5). Например, вы можете предложить ученикам обсудить:
• способы восприятия математики;
• способы представления идей;
• различные пути решения задач и реализации стратегий;
• выбранные методы: «Почему вы использовали эти методы? Как они работают?»
Когда ученики работают над открытыми задачами, они не только воспринимают математику как развивающую дисциплину, но и становятся исследователями. Они больше не ищут ответ; они анализируют идеи, устанавливают связи, развиваются и учатся. В процессе исследований они изучают формальную математику — методы и формулы, знания которых требует стандартная учебная программа. Разница в том, что они изучают стандартные методы, когда в них возникает необходимость, что пробуждает мотивацию и заинтересованность в изучении этих методов (Schwartz & Bransford, 1998). Как я уже подчеркивала, лучшие открытые задачи по математике — те, которые относятся к категории «низкий пол, высокий потолок» (см. сборник задач на сайте YouCubed — http://www.youcubed.org/tasks). На мой взгляд, чтобы понять, является ли задача открытой, нужно задать важный вопрос: обеспечивает ли она пространство для обучения?
Призывайте учеников быть математиками
Математики считают свою дисциплину творческой, красивой и эстетичной. Все дети могут работать так же, как математики, поэтому стимулирование их к тому, чтобы стать мини-математиками, может придать им уверенность в себе. Важно, чтобы ученики активно предлагали идеи — выдвигали математические гипотезы. Дебора Болл, которая сейчас занимает должность декана педагогического факультета Мичиганского университета, — одна из самых удивительных учительниц, с которыми я когда-либо встречалась. Дебора учила своих третьеклассников быть математиками: становиться исследователями и выдвигать гипотезы. Выработав единое мнение по поводу той или иной математической концепции, ученики ее класса говорили, что у них есть «рабочее определение», а затем уточняли его в рамках дальнейших исследований. Во время одного урока мальчик Шон выдвинул предложение по поводу числа 6, заявив, что оно может быть и четным, и нечетным (видео можно посмотреть здесь: Mathematics Teaching and Learning to Teach, 2010; http://deepblue.lib.umich.edu/handle/2027.42/65013).
Основанием для этой гипотезы послужило то, что число 6 состоит из нечетного количества чисел 2, а другие четные числа, например 4 и 8, имеют в своем составе четное количество чисел 2. Многие ученики вступили в спор с Шоном, вернувшись к рабочему определению четного числа, которое было выработано классом. Большинство учителей сказали бы Шону, что он неправ, и пошли дальше, но Дебору заинтересовал ход его мыслей. Среди учеников началась оживленная дискуссия, которая захватила зрителей с разным образованием и убеждениями, в том числе учителей и математиков. Во время урока дети начали глубоко анализировать гипотезу Шона и ни разу не попросили учительницу сказать им, прав Шон или нет, что сразу же положило бы конец обсуждению. Третьеклассники попросили Шона доказать свою гипотезу и предложили контраргументы, воспользовавшись разными определениями четного числа, чтобы показать Шону, что 6 — только четное число, которое не может быть нечетным. В какой-то момент Дебора поняла, что Шон обратил внимание на такое свойство числа 6 и других чисел (таких, как 10), состоящих из нечетного количества двоек, у которого нет названия в математике. В итоге класс решил назвать такие числа «числами Шона». Шон сделал наблюдение, которое не было неправильным; он обратил внимание на то, что у некоторых чисел есть особые свойства. Во время дальнейших дискуссий в течение года ученики этого класса продолжали исследовать числа и ссылались на «числа Шона», когда встречали их. В отличие от многих третьеклассников, которых отталкивает процедурное представление математики, этим детям нравилась возможность делиться своими идеями, а также выдвигать гипотезы, при этом изучая формальную математику. Эти ученики с воодушевлением работали с гипотезами, рассуждениями и доказательствами и напоминали стороннему наблюдателю юных ученых (Ball, 1993).
Некоторых людей шокирует мысль о том, чтобы называть детей математиками, хотя они спокойно называют их юными художниками и учеными. А дело в том, что математика поставлена на своего рода пьедестал, о чем я говорила в главе 6. Нам необходимо бороться с представлением о том, что только люди, много лет изучавшие математику в высших учебных заведениях, должны выступать в качестве математиков. Мы должны прекратить оставлять опыт взаимодействия с истинной математикой на самый последний период обучения, магистратуру. Ведь к этому моменту многие теряют интерес к математике. Не существует более эффективного способа донести до всех мысль о том, что математика — широкая, исследовательская дисциплина, которой могут заниматься все без исключения, чем предложить детям стать математиками.
Преподавайте математику как науку о закономерностях и связях
Суть математики сводится к изучению закономерностей. Многие понимают, что имеют дело с закономерностями, работая над такими задачами, как на рис. 9.3, в которых им предлагают продолжить закономерность.

Рис. 9.3. Полоса закономерности