Развитие технологий привело к тому, что индивидуальный подход к обучению математике получил более широкое распространение. Основатель Khan Academy Сал Хан — знаменитый приверженец индивидуального обучения. Он справедливо подчеркивает примитивность деления на группы по успеваемости и показывает, как ученики, которым дается возможность самим выбирать материал и путь обучения, добиваются гораздо больших успехов, независимо от начального уровня (Khan, 2012). Другие компании, работающие на основе современных технологий, также создали продукты, позволяющие ученикам заниматься на своем уровне. Однако, как ни печально, я еще не встречала такой продукт для индивидуальной работы, который обеспечит эффективное обучение математике. Но сам принцип предоставления ученикам возможности формировать свой путь обучения и получать индивидуальный материал в сочетании с условиями для групповой работы и сотрудничества позволяет предлагать задания высокого уровня всем ученикам.
Эффективное преподавание в смешанных группах: комплексное обучение
Задачи по математике, которые используются в смешанных группах, очень важны. Но не менее важны и правила, и ожидания в отношении того, как ученики должны работать вместе. Опытные учителя знают, что групповая работа на уроках может закончиться неудачей, если ученики принимают в ней неравноценное участие. Если дети предоставлены себе и их никто не стимулирует к формированию эффективных правил работы в группе, скорее всего, произойдет вот что: некоторые возьмут на себя большую часть работы, другие будут сидеть сложа руки, а кого-то вообще могут не допустить к работе, потому что они не имеют авторитета в глазах других. Социолог Стэнфордского университета Элизабет Коэн проанализировала закономерности неравного участия в групповой работе во время уроков и пришла к выводу, что это связано с социальными различиями между членами группы: некоторым ученикам присваивают или они сами принимают статус важных участников группы, а на других навешивают ярлык низкого статуса (Cohen, 1994). Моя коллега из Стэнфорда Дженнифер Лэнгер-Осуна изучила много примеров групповой работы, в которых основанием для рассмотрения идей был воспринимаемый статус ученика, который их выдвигает, а не математическое содержание (Engle, Langer-Osuna, & McKinney de Royston, 2014). Она пришла к выводу, что различия в статусе часто обусловлены стереотипными установками в отношении учеников определенной расы, социального положения или пола (Esmonde & Langer-Osuna, 2013; Langer-Osuna, 2011). Лиз Коэн и Рейчел Лотан разработали комплексный педагогический подход, направленный на обеспечение равенства в процессе групповой работы. Его можно использовать в любом классе и в преподавании любого школьного предмета (Cohen & Lotan, 2014).
В ходе четырехлетнего научного исследования, которое финансировал Национальный научный фонд, я сравнила разные подходы к преподаванию математики. Вместе с командой своих студентов я отслеживала успехи более 700 учеников разных старших школ (Boaler, 2008; Boaler & Staples, 2005). Примерно половину участников составляли ученики школ, в которых классы формировались по принципу успеваемости, преподавание математики носило формальный характер, а уровень знаний оценивался с помощью тестов. Другая половина участников — ученики городской школы в Калифорнии, которую я назвала Рейлсайд. В ней учителя отказались от деления учеников на группы по уровню успеваемости и преподавали математику в рамках комплексного подхода. Состав учеников этой школы был очень разнородным; в ней было больше учеников, изучающих английский язык, и более высокий уровень культурного многообразия, чем в любой другой школе. В Рейлсайд было примерно 38% учеников-латиноамериканцев, 23% афроамериканцев, 20% белых, 16% учеников азиатского происхождения и выходцев с тихоокеанских островов, 3% представителей других групп. В начале нашего исследования, когда ученики только окончили среднюю школу, мы организовали оценку уровня знаний по математике за прошедший период. В то время успеваемость учеников Рейлсайд была гораздо ниже по сравнению с другими городскими школами, принимавшими участие в исследовании, что не так уж нетипично для городской среды, в которой ученикам приходится решать много жизненных проблем (рис. 7.1).
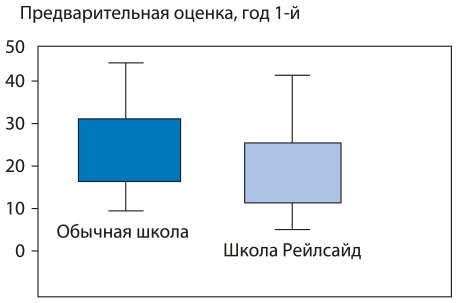
Рис. 7.1. Результаты предварительной оценки уровня знаний
Через год ученики Рейлсайд догнали тех, которые учились традиционным способом (рис. 7.2). Через два года их уровень успеваемости стал гораздо выше (рис. 7.3).
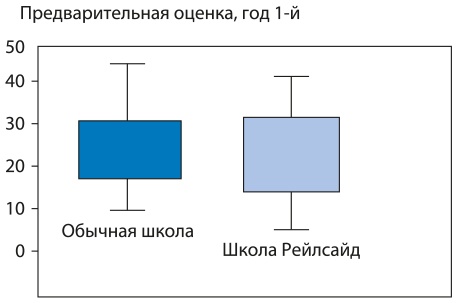
Рис. 7.2. Результаты оценки уровня знаний, год 1-й
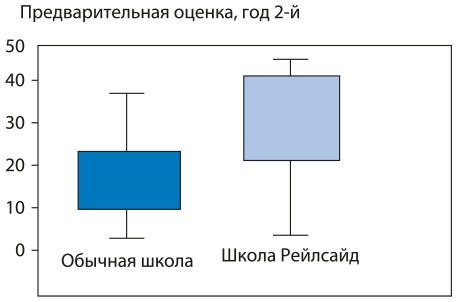
Рис. 7.3. Результаты оценки уровня знаний, год 2-й
Кроме того, ученики Рейлсайд получали гораздо большее удовольствие от математики и продолжили изучать этот предмет на более высоком уровне. В школе 41% учеников прошли углубленный курс начал анализа и анализа (из тех, кто обучался традиционным способом, таких было 27%). Кроме того, в Рейлсайд снизилось или исчезло расовое неравенство в плане успеваемости учеников (YouCubed at Stanford University, 2015a).
Не так давно была опубликована важная книга, посвященная анализу достижений Рейлсайд и применяемых в ней справедливых методов обучения, которую написали учителя этой школы (Nasir, Cabana, Shreve, Woodbury, & Louie, 2014).
Ниже представлен анализ того, как школе удалось добиться таких впечатляющих результатов, придерживаясь четырех принципов комплексного обучения: многоплановости, распределения ролей, присвоения компетенции и коллективной ответственности учеников (рис. 7.4).
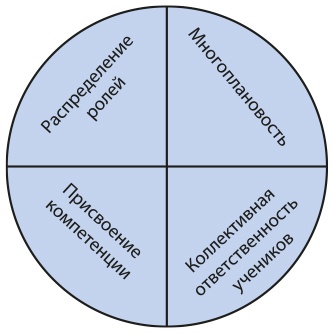
Рис. 7.4. Комплексное обучение
Многоплановость
Одноплановые уроки математики, широко распространенные в США, — это уроки, на которых практика ценится превыше всего и цель состоит в правильном выполнении процедур. Такой узкий критерий успеха приводит к тому, что некоторые ученики поднимаются на самый высокий уровень, получая хорошие оценки и похвалу учителя, а другие опускаются на самый низкий, причем большинству учеников известно их место в иерархии. Такие уроки одноплановые, поскольку на них есть только один способ добиться успеха. На многоплановых уроках математики учителя используют все методы работы.
Например, дети выполняют вычисления, а вдобавок задают интересные вопросы, предлагают идеи, устанавливают связи между разными методами, используют много разных форм представления, выстраивают цепочки логических рассуждений и предпринимают много других действий. Математика — широкая и многоплановая дисциплина. В классах, где применяется комплексный метод, учителя оценивают знания учеников по многим аспектам математики. На стенах классных комнат школы Рейлсайд был вывешен такой девиз комплексного обучения:






