Не так давно в рамках подготовки моего онлайн-курса я вместе со своими студентами взяла ряд интервью у прохожих Сан-Франциско. Мы опросили тридцать горожан разного возраста, этнической принадлежности и социально-экономического положения. Все интервью мы начинали с вопроса: «Скажите, пожалуйста, как вы относитесь к математике?» И все без исключения респонденты сразу начинали рассказывать, какие оценки по математике они получали в школе. Этого не произошло бы, если бы мы спросили прохожих, как они относятся к искусству, естественным наукам или литературе. Но в жизни людей, которые воспитывались в культуре достижений, математика сыграла жестокую роль инструмента оценки их ценности.
Я знакома со многими родителями, которые спокойно относятся к успехам своих детей в изучении английского языка, естественнонаучных дисциплин и других школьных предметов, но очень беспокоятся по поводу математики. Как правило, такие родители хотят, чтобы их дети как можно быстрее приступили к изучению высшей математики и проходили углубленные курсы, как будто иначе они начнут отставать или потеряют преимущество. Это прискорбно. Ведь мы знаем, что именно дети, которые углубленно изучают математику с раннего возраста, чаще прекращают заниматься этой дисциплиной, едва у них появляется такая возможность, и добиваются меньших успехов. Билл Джейкоб — профессор математики и заместитель председателя ученого совета Калифорнийского университета. Когда руководители школьных округов и родители задают ему вопрос об ускоренном переходе учеников к углубленному изучению математики, он рекомендует не делать этого в раннем возрасте, и говорит, что поспешность в изучении анализа часто приводит к более слабой подготовке, а также к тому, что ученики рано бросают курсы и в итоге это наносит им вред (Jacob, 2015). Кроме того, по данным Джейкоба, углубленный курс анализа не продвигает учеников вперед в области математики. Гораздо эффективнее оказывается более тщательное изучение основ. В университетах высоко ценят учеников, которые изучают анализ в старших классах, но на самом деле нет никакой необходимости спешить с углубленным изучением математики только ради более привлекательного аттестата. Кроме того, курс анализа не обязателен; многие мои студенты из Стэнфорда (даже те, которые изучают дисциплины категории STEM) не проходили его в старшей школе. Не так давно в мой кабинет в Стэнфорде пришла женщина, которая хотела пожаловаться на то, что ее школьный округ расформировал классы с углубленным изучением математики, чтобы все ученики могли изучать ее на углубленном уровне. Эта женщина начала агрессивно обвинять меня за принятые ее округом решения, но в ходе нашей беседы она испытала бурю эмоций, в том числе чувство облегчения. Сначала она сказала, что будущее ее дочери разрушено, поскольку она не может пройти курсы углубленного изучения математики. Я объяснила, что ее дочь по-прежнему может изучать математический анализ и в любом случае будет осваивать на уроках математику более высокого уровня; а если ей нужны сложные и интересные задачи, то глубокое изучение математических концепций принесет ей больше пользы, чем ускоренный переход к изучению более продвинутого материала. В итоге женщина успокоилась и покинула мой кабинет приободренной, но все же планируя обучать свою дочь дома — только математике.
Традиционные методы преподавания математики и культура достижений, которая просочилась в структуру преподавания и изучения этой дисциплины, вредят как сильным, так и слабым ученикам. Исследования показывают, что многие ученики с высокой успеваемостью прекращают заниматься математикой, а перевод учеников в группы более высокого уровня приводит к снижению концептуального понимания (Paek & Foster, 2012). Не так давно Джефф Смит, руководитель координационного совета Британской и Международной математической олимпиады, публично заявил по поводу поспешного перевода учеников на более высокий уровень, что это «катастрофа» и «ошибка», а сильным ученикам следует глубже изучать математику, вместо того чтобы быстро переходить на более высокие уровни. Но существует еще один аспект негативного влияния культуры достижений на учеников с высокой успеваемостью. Он отражается в количестве учеников, которые делают неправильный выбор в отношении будущего. Проведенное в Англии исследование показало, что студенты выбирали математику как дисциплину, которую они будут изучать в университете, потому что всегда были сильны в ней и чувствовали себя особенными. Но в университете обнаруживали, что их окружают столь же сильные студенты, и испытывали кризис идентичности (Wenger, 1998). В окружении таких же «особенных» они теряли уверенность в себе и понимали, что сама по себе математика им никогда не была интересна (Solomon, 2007). С другой стороны, сотни студентов могли бы изучать математику и получать удовольствие от этого, но отказались от такой возможности под влиянием ложных стереотипов, которые им внушили в школе.
Исполнительный директор YouCubed Кэти Уильямс до перехода в Стэнфорд много лет была руководителем направления математики в школьном округе. По работе она встречалась со многими родителями, которые утверждали, что их детям нужно давать материал посложнее, поскольку они продвинутые и умные. Кэти всегда предлагала встретиться с учениками и проводила тест на оценку уровня знаний по математике, который помогал ей определить их потребности. В итоге она неизменно приходила к выводу, что эти ученики хорошо владеют «техническими» аспектами, но не могут уловить смысл математических концепций или объяснить, почему они работают. Например, ученики могли разделить 1 на 3/4 и получить ответ, но не были способны объяснить, в чем его суть.
Кэти объясняла родителям, что математика — обширная дисциплина, которая выходит за рамки скоростных вычислений и процедур и подразумевает понимание концепций. Она показывала им рисунок, на котором изображены три аспекта математики (рис. 6.1).
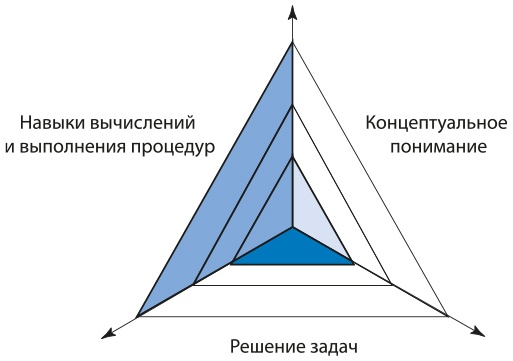
Рис. 6.1. Уравновешивание различных аспектов математики
Затем Кэти объясняла родителям, что их дети сильны в одной области математики и только начинают осваивать другие. Им нужно не столько изучать дополнительный материал, сколько понять тот, который они уже освоили, выйти за рамки многократного повторения одних и тех же процедур и научиться применять математические концепции на практике. Как показано в главе 3, именно эти аспекты математического мышления находятся в верхних строках списка требований работодателей.
Учителя не виноваты в том, что культура элитизма и достижений так распространена в сфере математики: ведь о них, как и об учениках, судят по их достижениям. Виновата культура, в которой математике отводится роль механизма отбора и показателя одаренности.
Нужно, чтобы она превратилась в открытую, обучающую дисциплину, рассчитанную как на сильных учеников, которые сейчас отказываются изучать ее, так и на слабых, не имеющих доступа к тем предметам, которые они вполне могут освоить. Многие согласны с тем, что ученикам необходима установка на позитивное мышление. Но если мы действительно хотим донести эту мысль до них, нам стоит изменить методы подачи и преподавания математики. Я заканчиваю все свои электронные письма подписчикам YouCubed словами «Да здравствует революция!» И нам действительно нужна революция — подразумевающая изменение убеждений в отношении математики как дисциплины, а также потенциала и мышления учеников. Она подразумевает отказ от элитизма и переход от получения результатов к обучению. Эта революция подразумевает принятие математики как многоплановой, красивой дисциплины, которая доступна всем.



