Упражнение
Нарисуйте стрелочную диаграмму для ИСР (рис. 8.5). Одно из решений приводится в разделе
«Ответы на вопросы»
.
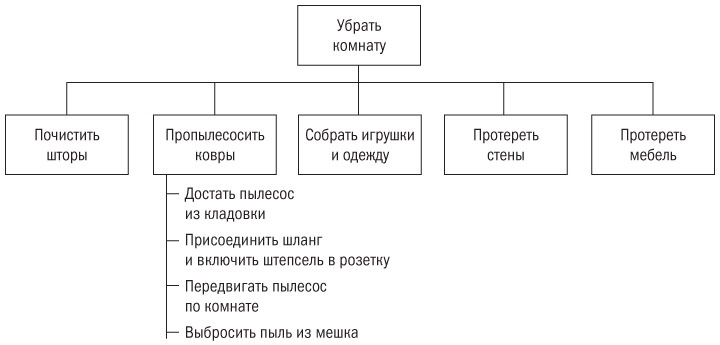
Рис. 8.5. ИСР по уборке комнаты
Глава 9. Создание рабочего расписания проекта
После того как вы подготовили соответствующую сетевую диаграмму расписания проекта, в которой определена продолжительность всех работ, нужно определить, где в ней расположен самый длинный путь (отрезок), и понять, соответствует ли он дате завершения проекта. Поскольку этот самый длинный отрезок определяет минимальную продолжительность проекта, любые работы на нем вызовут смещение даты окончания всего предприятия. Поэтому этот путь называется критическим путем.
Расчет расписания проекта
Обычно расчет расписания проекта делает компьютер. Однако я уверен, что, пока вы не поймете, как осуществляются эти расчеты, вы не поймете и значение резервов времени, назначения более ранних и более поздних дат и т. д. Более того, вы рискуете стать жертвой механизма «мусор на входе – мусор на выходе». Поэтому я вкратце расскажу, как расчет расписания делается компьютером. (В большинстве программ компьютер сам переводит время в календарные даты, что не так легко сделать вручную.)
Первое: подумайте о том, что нам нужно знать о проекте. Если он начинается в некое время = 0, мы хотим знать, когда он может быть завершен. В живых и актуальных проектах нам всегда называют дату, к которой он должен быть закончен. То есть дату окончания проекта нам диктуют. Кроме того, начало проекта всегда имеет обременения: не готовы ресурсы, не написаны спецификации или к этому моменту еще не завершился другой проект. Так что составление расписания проекта обычно представляет собой попытку вместить работу между двумя точками во времени. Несмотря на это, мы все же хотим знать, сколько нужно времени до исполнения проекта. Если это время не вписывается в требуемые временные рамки, придется что-то делать с сокращением критического пути.
В самом простом варианте расчет сетевой диаграммы расписания проекта делается исходя из предположения, что продолжительность всех работ по проекту точно соответствует заданию. Однако их продолжительность зависит от уровня обеспеченности работ ресурсами, а если к моменту начала ресурсов в действительности будет не хватать, нереальны и даты решения задач, указанные в расписании.
Именно по этой причине расчет сетевой диаграммы расписания проекта должен осуществляться с учетом возможной ограниченности ресурсов. Другими словами, распределение ресурсов необходимо для того, чтобы понять, какое именно расписание проекта выполнимо! Неудачное определение ресурсов по проекту почти всегда приводит к невыполнимости расписания.
Таким образом, первым делом в расчете сетевой диаграммы расписания нужно определить критический путь и возможный объем некритических работ при идеальных условиях. Разумеется, идеальны условия, при которых проект обеспечен неограниченными ресурсами, поэтому первые расчеты сети расписания совершаются без учета возможных требований с точки зрения ресурсов. Этот метод описан в данной главе, а вопросы распределения ресурсов рассматриваются в руководствах по программному обеспечению подготовки расписаний.
Правила сети расписания проекта
Для расчета времени начала и окончания сети расписания проекта применяются только два правила: правило 1 и правило 2. Другие правила компьютерные программы могут применять сами. Обычно, это функция конкретной программы, поэтому не имеет отношения ко всем сетям.
ПРАВИЛО 1. Прежде чем начнется выполнение конкретной задачи или работы, все предшествующие работы должны быть завершены.
ПРАВИЛО 2. Стрелки обозначают логический порядок работ.
Базовые расчеты расписания
Расчеты расписания проиллюстрированы в диаграмме сети (рис. 9.1). Сначала внимательно посмотрим на квадратики в диаграмме. В каждом из них содержатся сокращения РС, ПС, РФ, ПФ и ПР.
РС – ранний старт;
ПС – поздний старт;
РФ – ранний финиш;
ПФ – поздний финиш;
ПР – продолжительность (выполнения работы или решения задачи).
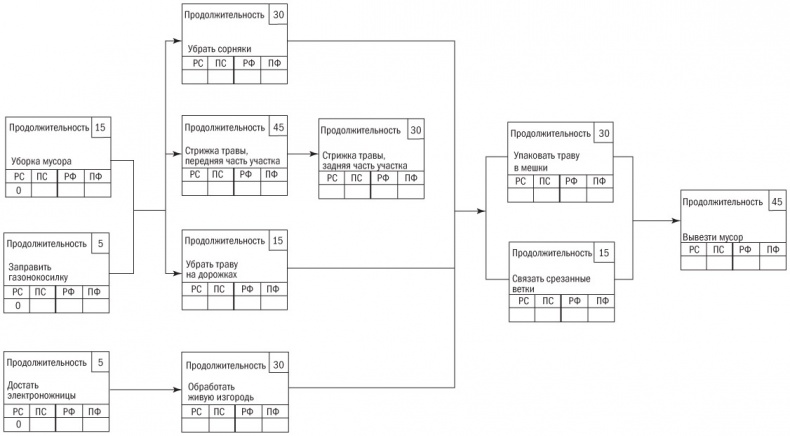
Рис. 9.1. Сеть расписания, которая иллюстрирует принципы его расчета
Вычисления с направленностью вперед
Посмотрите на какую-нибудь отдельную работу, внесенную в сеть расписания, например уборку мусора на участке. Ее продолжительность 15 минут. Если предположить, что она начнется с временной точки 0, то может быть закончена через 15 минут. Значит, мы можем внести число 15 в ячейку, помеченную как РС.
Заправка бензином газонокосилки и культиватора для устранения сорняков занимает всего пять минут. Логика диаграммы говорит нам, что обе эти задачи должны быть выполнены до того, как мы начнем выпалывать сорняки, косить траву и убирать ее с дорожек. Уборка мусора занимает 15 минут, а заправка косилки и культиватора – только пять. Когда могут быть начаты следующие работы? Только тогда, когда закончится уборка мусора, потому что это самая продолжительная задача из первых работ.
Ранний финиш уборки мусора становится ранним стартом других работ. Всегда действует порядок: ранний финиш начальных работ становится ранним стартом работ последующих. То есть самый длинный отрезок первых работ определяет, как рано могут начаться следующие работы.
Следуя этому правилу, мы можем внести время раннего старта для каждой задачи (рис. 9.2). В результате узнаем, что для завершения всего проекта нам нужно 165 минут, если работы будут выполняться в соответствии с диаграммой сети расписания. Мы только что осуществили вычисления с направленностью вперед, чтобы определить по всем задачам их самые ранние стартовые точки. Компьютерные программы делают то же самое и в дополнение к этому переводят время в календарные дни.
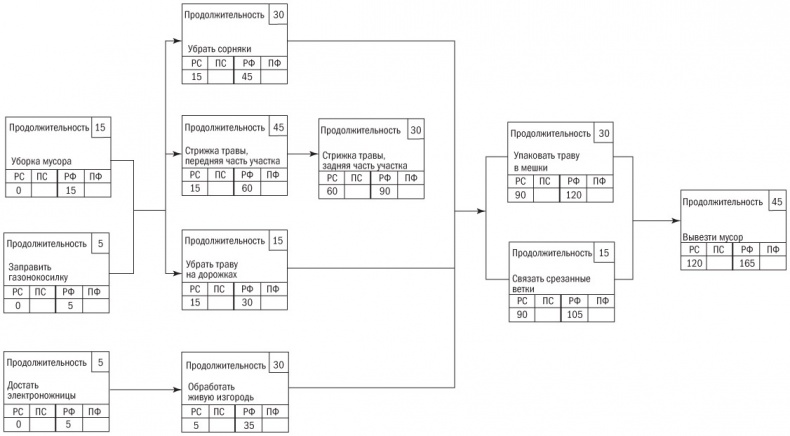
Рис. 9.2. Сетевая диаграмма расписания с указанием ранних финишей
ПРАВИЛО. Когда две или более работ или задач предшествуют другой задаче, самое раннее время ее начала определяется наибольшей продолжительностью предшествующей работы.

