Теперь мы понимаем, как можно заниматься логикой с помощью электродинамики. Рассмотрим простейший случай. Допустим, что к проводнику, конец которого мы обозначим буквой q, приложено так называемое рабочее напряжение. Происходит только это, и насчет конца q можно сказать лишь то, что к нему относительно земли (потенциал которой считают равным нулю) приложено некоторое напряжение. Поэтому данный факт обозначают тем, что приписывают q значение единица, то есть q = 1. Если, однако, соединить участок проводника вблизи q со вторым проводником, тоже заземленным, то через соединение и второй проводник в землю потечет ток благодаря источнику напряжения, и напряжение на конце q станет равным 0. Теперь в игру вступает транзистор: он подключен к схеме так, что часть проводника от узлового соединения до транзистора есть К, а часть проводника от транзистора до земли есть Э. Теперь все зависит от того, имеется ли напряжение на базе Б, которое мы обозначим буквой p. Если напряжение есть, то мы пишем p = 1, если же его нет, то мы пишем p = 0. Если p = 1, транзистор пропускает ток от К к Э, а на конце q напряжение отсутствует, то есть q = 0. Когда же, наоборот, p = 0, транзистор заперт, ток через него прекращается, а на конце qвозникает напряжение, то есть q = 1.
Данный электротехнический элемент символизирует логическое отрицание: q означает «не-p». Если эти элементы включить параллельно или последовательно, то можно получить все логические операции. Например, можно составить отношение «ни p, ни q» (логический вентиль «ИЛИ-НЕ»). На конце проводника r будет напряжение только тогда, когда нет напряжения ни на проводнике, символизирующем высказывание p, ни на проводнике, символизирующем высказывание q. Другими словами, только при p = 0 и при q = 0 будет r = 1, то есть это значение r соответствует положению «ни p, ни q». То есть r соответствует ситуации, когда высказывания p и q являются одновременно ложными. Если же, напротив, p = 1 и q = 0, или p = 0 и q = 1, или даже p = 1 и q = 1, то r = 0, ибо «ни p, ни q» является ложным высказыванием, если одно из них, либо p, либо q, является истинным
.
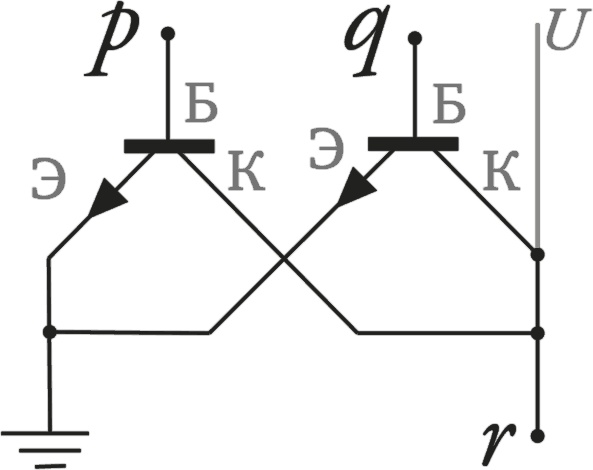
Рис. 7. Принцип работы вентиля «ИЛИ-НЕ». Только при p = 0 и при q = 0 будет r = 1, ибо только в этом случае оба транзистора не проводят в землю ток при приложении напряжения U. Во всех остальных случаях ток проводится и r = 0
Пара таких подключений — и на устройстве можно выполнять вычисления такие же, как на машине Паскаля
. Если же таких каскадов будет большое множество и они будут соответствующим образом подключены друг к другу, то мы получим настоящую, современную вычислительную машину. Если вычисления производятся по программе, состоящей из однозначно определенных действий с символами, то машине вполне по силам ее выполнить.
Скептицизм Гелернтера и тест Тьюринга
Уотсон, победивший Кена Дженнингса и Брэда Раттера в игре «Jeopardy!», как раз и был такой числовой машиной. В ней хранились данные, закодированные в виде исполински длинных последовательностей цифр 0 и 1. Эта цифровая последовательность, преобразованная в совокупность имеющегося напряжения для обозначения 1 и отсутствия напряжения для обозначения 0, и есть сомнительный источник «знания» Уотсона. Технологический шедевр заключается в том, что это устройство создает иллюзию умения машины думать.
Редакторы новостного журнала Spiegel были настолько очарованы Уотсоном, что решили расспросить о нем какого-нибудь выдающегося специалиста по вычислительным машинам. Их выбор пал на Дэвида Гелернтера, создавшего в 1983 г. вместе со своим коллегой Николасом Карьеро язык программирования LINDA, который хорошо подходил для параллельно работающих вычислительных машин. Суть беседы репортеров Spiegel с Гелернтером заключалась в следующем диалоге:
Spiegel. Господин Гелернтер, мы хотим отгадать одно понятие. Американский журналист Амброуз Бирс описал его так: «Преходящее безумие, излечивающееся браком». Вы знаете, что он имел в виду?
Дэвид Гелернтер. Даже не догадываюсь.
Spiegel. Это любовь.
Дэвид Гелернтер. О, любовь!
Spiegel. Да, этот вопрос был задан на шоу «Jeopardy!». Суперкомпьютер Уотсон без проблем дал правильный ответ. Это может означать, что Уотсон знает, что такое любовь?
Дэвид Гелернтер. Он не имеет о любви ни малейшего представления. Исследования в области искусственного интеллекта пока ни разу не касались человеческих чувств. Проблема заключается в том, что мы мыслим не только рассудком. Мы мыслим духом, который к тому же обладает телом. Такое чувство, как любовь, намного превосходит мыслительные способности Уотсона.
Spiegel. Что же в человеческом мозге такого особенного, что не позволяет создать машину по его образу и подобию?
Дэвид Гелернтер. Мозг коренным образом отличается от компьютера. Компьютер — это чисто электронный механизм, состоящий из полупроводников и прочего электрического хлама. Я верю, что можно создать машину, способную к творчеству, вероятно, можно даже сделать машину, способную галлюцинировать. Но такая машина нисколько не будет похожа на нас. Это будет лишь обманчивый фасад. Можно, если пофантазировать, представить себе, что модель «Уотсон-2050» выиграет поэтический конкурс. Возможно, он напишет чудесный сонет, который я найду прекрасным и трогательным и который в веках обессмертит имя его создателя. Но будет ли это означать, что Уотсон напишет сонет, движимый какой-то оригинальной, самостоятельной идеей? Естественно, нет. В доме никого нет. В нем никто не живет.
Скепсис Дэвида Гелернтера немного напоминает прозрение Блеза Паскаля относительно того, что мы мыслим не только за счет законов формальной логики, но прежде всего сердцем: «Le cœur a ses raisons que la raison ne connaît pas» — «У сердца есть основания, неведомые рассудку».
Тем не менее Мински и Моравек искренне полагали, что в достаточно сложно сконструированной числовой машине можно найти нечто, напоминающее истинное мышление. Правы они или нет? Для того чтобы ответить на этот вопрос, британский математик и логик Алан Тьюринг в 1950 г. предложил провести тест. В ходе этого теста, названного в честь Тьюринга, испытатель с помощью компьютерной клавиатуры и монитора, не имея никакого зрительного и слухового контакта с собеседниками (их двое), ведет с ними разговор. Один собеседник — человек, второй — машина. Оба собеседника стараются убедить испытателя, задающего им вопросы, в том, что они являются мыслящими существами. Если после интенсивного обмена репликами испытатель не сможет отличить человека от машины, то она считается выдержавшей тест Тьюринга.

