Основными экспериментами по непрямым поискам темной материи являются: космический эксперимент PAMELA, аппаратура которого размещена на российском спутнике «Ресурс-ДК1», космический гамма-телескоп FERMI–LAT, космический телескоп EGRET на борту космического аппарата CGRO и недавно доставленный на МКС альфа-магнитный спектрометр AMS-02, а также эксперимент ATIC, аппаратура которого запускалась на аэростате в Антарктиде.
К сожалению, среди непрямых экспериментов противоречий еще больше, чем среди прямых. Есть еще одно направление непрямого поиска частиц темной материи. При анализе данных спектра рентгеновского излучения из космоса был обнаружен неизвестный ранее пик в районе энергии 3,5 кэВ. Некоторые ученые уверяют, что это излучение, возникшее при аннигиляции подобных частиц с их античастицами, хотя другие считают, что это ничем не примечательная линия излучения известных химических элементов.
Как видим, поисками темной материи вплотную занялись экспериментаторы, хотя пока что безрезультатно. Впрочем, характеристики детекторов постоянно улучшаются, и уже в недалеком будущем можно ожидать одно из трех: либо будут открыты вимпы или что-то похожее на них, что со временем становится все менее вероятным, либо порог их обнаружения будет понижен настолько, что заставит теоретиков пересмотреть свои предсказания (правда, у них в запасе всегда есть принципиально ненаблюдаемые варианты), либо разные эксперименты будут противоречить друг другу, и тогда этот спор может затянуться не на один десяток лет.
Следует отметить, что отрицательный результат экспериментов не означает, что нет никакой темной материи. Формально это означает только то, что сечение ее слабого взаимодействия находится ниже порога обнаружения или масса вимпов сильно отличается от ожиданий. Возможный вывод заключается в том, что темная материя не участвует в слабом взаимодействии и состоит из стерильных нейтрино или чего-то подобного.
4.4. Альтернативные модели
Итак, астрономических наблюдений, подтверждающих существование темной материи, достаточно много. Но можно ли их объяснить каким-то иным образом без привлечения идей темной материи? Для многих это действительно так, хотя и не для всех. Темная материя необходима для роста крупномасштабной структуры Вселенной. Но для того, чтобы объяснить наблюдения, не привлекая темную материю, приходится жертвовать более фундаментальными вещами. Например, существует гипотеза, объясняющая кривые вращения галактик тем, что при малых значениях ускорения нарушается второй закон Ньютона. Эта так называемая модифицированная ньютоновская динамика (MOND) имеет небольшое число сторонников, хотя и очень активных. Подумаем, к каким последствиям приведет такая гипотеза. Для начала надо отказаться от классической механики и заменить ее на какую-то пока не разработанную теорию. Соответственно, рушится фундамент всей физики. Слабые ускорения могут быть связаны с взаимодействиями в рамках молекулярной физики, физики твердого тела, физики элементарных частиц и во многих других областях. Все эти науки придется перестроить без каких-либо на то экспериментальных оснований только для того, чтобы объяснить кривые вращения галактик. При этом остальные доказательства существования темной материи не могут быть объяснены в рамках MOND. Для них придется придумать какие-то другие гипотезы. Гипотеза же о темной материи хороша тем, что объясняет единым образом много различных экспериментов. Другой идеи, подходящей для всех случаев, пока не существует.
Глава 5
Темная энергия
5.1. Космологические свидетельства существования темной материи и темной энергии
Перейдем от масштабов галактик, т. е. астрономических, к масштабам космологическим. Это позволяет решить несколько задач. Во-первых, получить независимые оценки Ωm – плотности материи, выраженной в процентах от критической плотности. Во-вторых, разделить вклады темной и барионной материй. Для этого вводится аналогичный параметр Ωb – отношение плотности барионной материи к критической. Понятно, что плотность небарионной темной материи в процентах от критической плотности будет равна Ωm – Ωb. В-третьих, кроме этого, естественно получаются оценки параметра ΩΛ – отношения плотности энергии, связанной с космологической постоянной, к критической плотности энергии. В настоящее время космологическая постоянная рассматривается как один из частных случаев темной энергии, о которой мы расскажем ниже.
Еще до открытия реликтового излучения космологи мечтали о двух типах космических объектов, которые позволили бы им разобраться с геометрией пространства-времени, в частности определить знак кривизны Вселенной. Первый тип объектов получил жаргонное название «стандартная свеча». Это объекты, которые обладают одинаковой светимостью, но при этом находятся на очень разных расстояниях от Земли. Второй тип объектов называется стандартной линейкой и имеет одинаковые линейные размеры. Зачем эти объекты были так нужны? Дело в том, что в искривленном пространстве, как мы уже упоминали в разделе 2.5, понятие расстояния становится неоднозначным. Вводятся несколько видов расстояний, которые связаны друг с другом через кривизну пространства.
Имея стандартную свечу, мы можем ввести так называемое фотометрическое расстояние. По определению, это расстояние, на которое нужно в плоском пространстве отнести источник света, чтобы получить наблюдаемый поток света. Его отличие от обычного расстояния связано с двумя факторами. Первый из них связан с тем, что освещенность поверхности обратно пропорциональна квадрату расстояния до точечного источника света. Это справедливо только для плоского пространства. В пространстве с положительной кривизной поверхность сферы радиуса r меньше чем 4πr2. Соответственно, освещенность будет падать медленнее, чем r–2. Понятно, что в пространстве с положительной кривизной, где поток больше, чем в плоском пространстве, благодаря только первому фактору, фотометрическое расстояние будет меньше, чем в плоском. Соответственно, в пространстве отрицательной кривизны, где площадь поверхности сферы больше чем 4πr2, фотометрическое расстояние было бы больше, чем в плоском пространстве при одинаковых потоках.
Второй фактор связан с тем, что свет от удаленных источников был излучен в более ранней Вселенной и за время распространения длина его волны увеличилась в 1 + z раз. Соответственно, энергия фотонов, пропорциональная частоте, уменьшилась в 1 + z раз. Кроме того, в 1 + z раз увеличилось время между приходами фотонов. В результате в формуле для потока света, наблюдаемого на Земле, возникает множитель (1 + z)–2, что увеличивает фотометрическое расстояние в 1 + z раз.
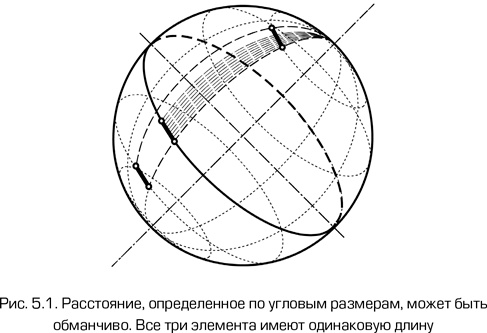
Имея стандартную линейку, мы можем ввести понятие расстояния, определенного по угловым размерам. В плоском пространстве объект длиной l на расстоянии r >> l виден под углом φ = l/r в радианной мере. Соответственно, расстояние может быть определено по формуле r = l/φ. В кривом пространстве все куда сложнее. Рассмотрим поверхность сферы, например Земли (см. рис. 5.1). Пусть наблюдатель находится на Северном полюсе и измеряет угловые размеры метровой линейки, расположенной точно вдоль параллели. Поскольку в двумерном пространстве с положительной кривизной свет распространяется по большому кругу, фактически нам необходимо вычислить разность долгот западного и восточного концов линейки. По мере удаления линейки от наблюдателя ее угловые размеры будут уменьшаться, достигнут минимума на экваторе, а затем снова начнут увеличиваться при приближении к Южному полюсу
[77]. При этом угловой размер линейки на экваторе будет равен 2π×1 м/40 000 км. В плоском же пространстве угловой размер линейки будет равен 1 м/10 000 км. Таким образом, в пространстве с положительной кривизной минимальный угловой размер линейки будет в π/2 ≈ 1,57 раз больше, чем в плоском, независимо от величины кривизны. Соответственно, расстояние по угловым размерам будет меньше, чем в плоском пространстве. В пространстве с отрицательной кривизной ситуация будет обратной: расстояние по угловым размерам будет больше, чем в плоском пространстве.



