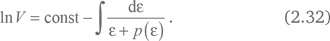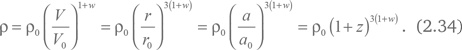Из уравнений (2.10) и (2.11) также следует, что
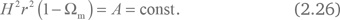
Ранее мы встречались с этой же формулой, но примененной к текущему моменту времени (2.15).
Обратите внимание, что из закона Хаббла (2.1) следует
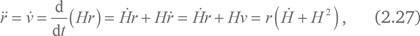
что означает, что

Таким образом, замедление означает не только уменьшение Н, оно означает, что qположительно и
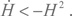 Величина Hr убывает при q > 0 согласно формулам (2.23) и (2.27). Это означает, что абсолютная величина отклонения Ωm от единицы увеличивается при расширении Вселенной. Эти отклонения положительны для закрытой модели и отрицательны для открытой. Только плоская модель остается все время плоской. В любом случае модели Фридмана без космологической постоянной, или темной энергии, обеспечивают увеличение величины |1 – Ωm|.
Величина Hr убывает при q > 0 согласно формулам (2.23) и (2.27). Это означает, что абсолютная величина отклонения Ωm от единицы увеличивается при расширении Вселенной. Эти отклонения положительны для закрытой модели и отрицательны для открытой. Только плоская модель остается все время плоской. В любом случае модели Фридмана без космологической постоянной, или темной энергии, обеспечивают увеличение величины |1 – Ωm|.
2.7.4. Материя с ненулевым давлением в расширяющейся Вселенной

Рассмотрим объем V, заполненный материей с плотностью энергии ε и давлением р. Оба параметра изменятся, если мы сожмем или расширим этот объем, и сделают они это согласованно. Зависимость между давлением и плотностью энергии называется уравнением состояния. Мы уже обсуждали это в разделе 1.3. Уравнение состояния называется баротропным, если давление является функцией только плотности энергии p = p(ε).
Начнем с получения зависимости этих величин от объема. Для случая пылевидной материи эта зависимость имеет вид (2.8). Для того чтобы получить ее для материи с баротропным уравнением состояния, мы используем закон сохранения энергии, он же первый закон термодинамики, который имеет вид
dE = dQ − dA. (2.29)
Здесь E = εV – внутренняя энергия материи, dE – ее изменение, dQ – количество тепла, поглощенного этой материей, а dA = pdV – механическая работа, совершенная материей в ходе ее расширения.
Термодинамический процесс с dQ = 0 называется адиабатическим. Он не сопровождается передачей тепла внутрь или наружу системы. Чтобы сделать процесс адиабатическим, в лабораториях используется специальное оборудование для предотвращения передачи тепла в ту или иную сторону. В повседневной жизни мы используем термос, чтобы горячие или холодные напитки хранились в практически адиабатических условиях. Но никто не нуждается в термосе, чтобы сделать адиабатическим космологическое расширение. Действительно, температура в однородной Вселенной везде одинакова, поэтому не происходит никакой передачи тепла из одного места в другое, а передача тепла наружу невозможна, ведь Вселенная не имеет никакого «снаружи».
С учетом этого уравнение (2.29) сводится к
dE = d(εV) = εdV +Vdε = −dA = − pdV, (2.30)
или
Vdε = –(ε + p)dV. (2.31)
Зная баротропное уравнение состояния p = p(ε), мы можем легко найти его решение:
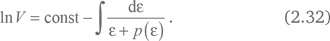
Особенно просто рассмотреть случай весьма популярного среди космологов уравнения состояния
p = wε, w = const. (2.33)
Из формул (2.32), (2.33) и учитывая, что V ~ r3, получаем:
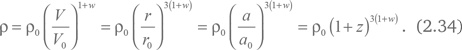
Здесь ρ0 – плотность материи в тот момент, когда сфера имела размер r0 или Вселенная имела масштабный фактор a0. В релятивистской космологии это просто настоящий момент, или «сейчас». Так, плотность материи ρ зависит от ее текущего значения ρ0 и отношения размеров, выраженного через красное смещение z. Случай пылевидной материи без давления соответствует w = 0. Подставляя это значение в уравнение (2.34), мы, как и следовало ожидать, получим уравнение (2.8).
Особый случай w = –1 или p = –ε дает интересный результат. Уравнение (2.31) гарантирует, что в этом случае плотность энергии постоянна. Расширение или сжатие Вселенной не меняет ни плотность энергии ε, ни плотность вещества ρ, ни его давление p. Этот случай описывает космологическую постоянную Λ.
2.8. Современная модификация модели
2.8.1. Космологическая постоянная наносит ответный удар
Решения Фридмана побудили Эйнштейна отказаться не только от теории статической Вселенной, но также и от идеи космологической постоянной, которую он впоследствии называл величайшей ошибкой в своей жизни, согласно воспоминаниям его коллеги – физика Георгия (Джорджа) Гамова
[36]. Тем не менее другие ученые, занимающиеся новой наукой о свойствах и эволюции Вселенной в целом – космологией, не спешили отказываться от космологической постоянной. Притом что к существованию Λ-члена космологи относились скептически, они рассматривали модели как без космологической постоянной, так и с ее учетом. Долгое время первый вариант хорошо описывал все астрономические данные, но потом ситуация изменилась. Астрономические наблюдения последних десятилетий подтвердили существование космологической постоянной и позволили измерить ее величину Λ = 1,19×10−52 м−2.
Космологическую постоянную Λ можно рассматривать как некоторый экзотический вид среды с постоянной плотностью энергии εΛ, давлением pΛ и плотностью вещества ρΛ, которые не изменяются в ходе космологического расширения. Причиной такого постоянства является отрицательная работа против отрицательной силы давления, которая сохраняет постоянство плотности энергии Вселенной ε = ρc2. И действительно, давление, создаваемое космологической постоянной, отрицательно и характеризуется значением



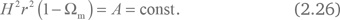
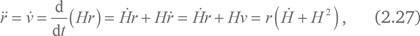

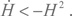 Величина Hr убывает при q > 0 согласно формулам (2.23) и (2.27). Это означает, что абсолютная величина отклонения Ωm от единицы увеличивается при расширении Вселенной. Эти отклонения положительны для закрытой модели и отрицательны для открытой. Только плоская модель остается все время плоской. В любом случае модели Фридмана без космологической постоянной, или темной энергии, обеспечивают увеличение величины |1 – Ωm|.
Величина Hr убывает при q > 0 согласно формулам (2.23) и (2.27). Это означает, что абсолютная величина отклонения Ωm от единицы увеличивается при расширении Вселенной. Эти отклонения положительны для закрытой модели и отрицательны для открытой. Только плоская модель остается все время плоской. В любом случае модели Фридмана без космологической постоянной, или темной энергии, обеспечивают увеличение величины |1 – Ωm|.