14.8.2
Применение незначимой информации
Ответьте, пожалуйста, на один вопрос. В ящике комода лежит 110 носков, черных и коричневых. Количественное отношение между черными и коричневыми носками 5 к 6, то есть на каждые пять черных приходится шесть коричневых. Вы с закрытыми глазами достаете носки по очереди, по одной штуке. Кладете носок на стол, и только потом смотрите, что достали. Потом закрываете глаза и достаете очередной носок. Сколько носков надо достать, чтобы получилась нормальная пара? Подумайте. Кто-то пишет 51, кто-то 10.
Если вы действительно стали думать, вы допустили еще одну ошибку – применение незначимого информации. Она отличается от первой тем, что здесь мы учитываем ту информацию, которая является простым шумом, создающим помехи, тратим на это время и энергию. В первом же случае мы неправильно выбираем сам критерий при принятии решения. Так какой травильный ответ? 3! Если первые два носка разного цвета, то третий, так как цветов только два, будет совпадать с одним из них. В каких ситуациях принятия решения вы используете незначимую информацию?
14.8.3
Влияние предыдущих установок
Отгадайте загадку.
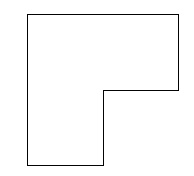
Рис. 52. Участок земли
У крестьянина было 4 сына и надел земли, изображенный на рисунке. Крестьянин был уже стар и решил отдать свою землю сыновьям. Но он не хоте л никаких раздоров между сыновьями из-за того, что получатся разные наделы для каждого. Поэтому крестьянин собрал всех своих сыновей и сказал: «Вы получите мою землю, если разделите надел на 4 цельных, равных по площади, размеру и по форме участка». Итак, вопрос вам понятен! Как разделить фигуру на рисунке на четыре цельные, равные по площади, размеру и по форме части? Не торопитесь смотреть в ответы! Попробуйте правильно структурировать задачу.
Итак, для тех, кто все-таки не ста л сам придумывать ответ, сделаю следующее направляющее замечание. Раздробите каждый маленький квадратик (фигура состоит из трех квадратов) на четыре четверти. Теперь посмотрите, что получилось. И если высказывание «полководец не принимает решение, полководец разглядывает победу» существует, то оно применимо именно к данной ситуации. Разглядите победу. Всмотритесь в то, что получилось, и наверняка вы увидите решение (рис. 53).
Правильное решение: 10-6-7, 3-4-8, 5-1-2, 9-11-12. Правильная структуризация задачи приводит к ее решению!
Продолжаем геометрические путешествия. Посмотрите на следующий рисунок! А теперь разделите то, что вы видите, на 6 равных частей (здесь длинная сторона в два раза длиннее, чем короткая) (рис. 54).
Ну как, получается? Думайте, думайте, думайте! Если на стенах офисов Coca Cola написано: «Если вы не позаботитесь о своем клиенте, то о нем позаботится кто-то другой», то на стенах офиса Microsoft начертано: Thinking. Думайте! Кстати сказать, вот она, корпоративная культура!
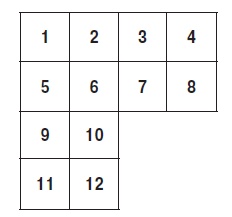
Рис. 53. Дробленый участок
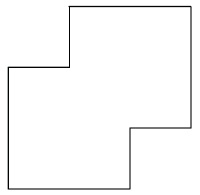
Рис. 54. Разделить на 6 равных частей
А что написано на стенах вашего офиса? Надеюсь, там не наклеены календарики с фотографиями кошечек?!
Ну, как? Получилось разделить на шесть частей? Если нет, то вы находитесь под влиянием распространенной ошибки – влияния предыдущих установок. Тот подход, который пригодился вам три решении задачи о четырех братьях, создал в вашей голове определенную внутреннюю установку. Она включается три решении внешне похожих задач. Но ведь внешнее сходство не гарантирует внутреннего равенства. Разумеется, нет. Повторю задачу. Разделите то, что нарисовано, на 6 равных частей. Подсказка, как это часто бывает, в самом вопросе. Вы видите нарисованный контур. Его можно разделить на 6 равных частей? Нет проблем! (рис. 56)
Часто установки, созданные решением предыдущей ПВ, влияют на разрешение следующей. И это может быть ошибкой.
14.8.4
Ограниченность рамками задачи и/или внутренними барьерами
Если вы не знаете следующей загадки, то хочется спросить, вы случайно не с Луны свалились? Кстати, как там, на Луне? Есть следы американских астронавтов? Или их высадка все-таки была инсценировкой?
Перед вами квадрат из девяти точек. Вам необходимо пересечь все точки четырьмя линиями, не отрывая руки от листа и не проводя дважды по одной и той же линии (линии, разумеется, могут пересекаться). Или можно по-другому сказать, что нужно пересечь все девять точек одной ломаной линией, состоящей из четырех прямых.

Рис. 55. Девять точек
Частая сложность, с которой сталкиваются люди при решении тех или иных ПВ, заключается в том, что мы воспринимаем ситуацию в пределах самой ситуации. Но ведь часто никто не накладывает никаких ограничений. Мы сами – клубок сплошных ограничений. Ограничения внутри нас. Вот, к примеру. Представьте себе следующее. Вы берете стеклянную банку, чтобы видеть, что внутри. Кладете туда кузнечика, чтобы он прыгал. И накрываете банку картонкой, чтоб он не выпрыгнул. Не забудьте сделать в картонке маленькую дырочку, чтоб кузнечик не задохнулся. Теперь наблюдайте. Кузнечик прыгает, прыгает, прыгает, прыгает, прыгает и в какой-то момент перестает прыгать. Вы снимаете картонку, а он все равно не прыгает! Почему? Кузнечик выработал рефлекс барьера. Внешнее препятствие стало внутренним. Как говорил Ланцелот, «дракон не там где-то, дракон внутри нас», убить дракона! Это явление, когда внешняя преграда превращается во внутреннюю, называется выученной беспомощностью. Внешний барьер превращается во внутренний.
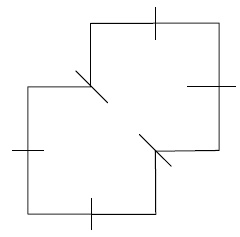
Рис. 56. Равные части
Внешний уже давно исчез, а внутренний остается надолго. Это один из возможных психологических механизмов появления бессознательного самоограничения. Могут быть и другие механизмы, но сейчас для нас главное другое – то, что мы сами себе создаем барьеры, сами накладываем ограничения.
Выйдите за пределы квадрата, и решение будет.