Вопрос Архимеда заключался в следующем: какую часть цилиндра заполняет сфера?
(В действительности вопрос был более элементарным: насколько велика сфера? Но любое описание размера требует ссылки на что-то, что нам уже известно: к примеру, мой рост – это приблизительно 5 2/3
[55] тех давно существующих единиц, которые называются футами. И тут-то в дело как раз и вступает цилиндр.)
Для начала разрежем всю фигуру пополам. Вместо теннисного мяча в контейнере мы получим полусферу в хоккейной шайбе.
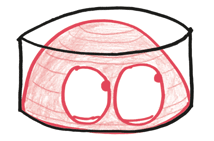
Теперь, вместо того чтобы беспокоиться об объеме внутри полусферы, мы можем сосредоточиться на объеме вне ее. В духе «бесчисленных бед» мы можем считать эту область пачкой обручей или шайб, каждая из которых является окружностью с круглой дырой в середине.
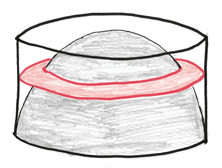
Внизу этой стопки находится чрезвычайно тонкая шайба. Ее дыра занимает весь круг, оставляя только напоминающее струну кольцо. Наверху тем временем пребывает очень толстая шайба. Это почти целый круг с отверстием размером с булавочный прокол. Между ними находится целое семейство шайб.
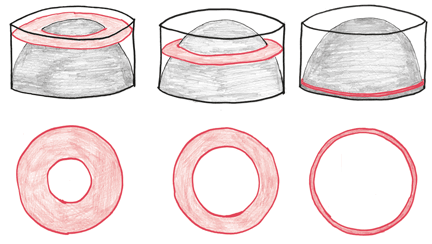
Каковы площади этих фигур? После интерлюдии с хитрой алгеброй мы приходим к выводу, что площадь каждой равна πh2, где h – расстояние от поверхности.
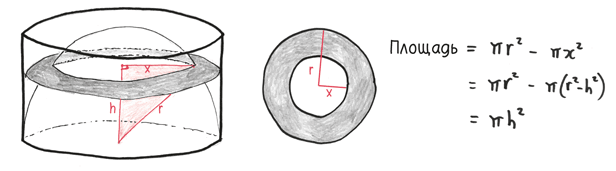
Это означает, что, применяя Принцип бесчисленных бед, каждую из них можно заменить кругом радиусом h.
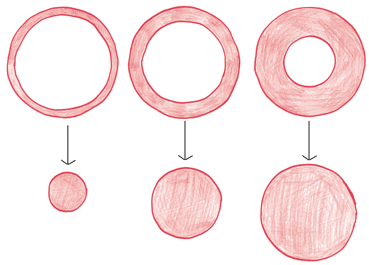
Видите! У нас получился не странный кратер в форме полусферы, а простой конус, перевернутый острием вниз.
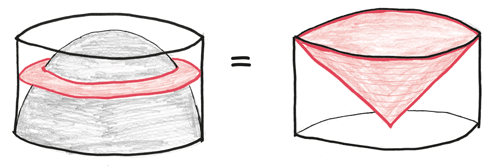
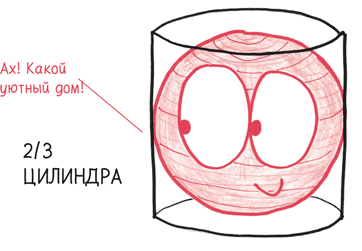
Как мы уже установили, конус заполняет 1/3 цилиндра. Таким образом, пустое пространство – то есть то, что было полусферой – заполняет 2/3.
Вывод: сфера заполняет 2/3 цилиндра.
Над этими чертежами на сицилийском песке Архимед мечтал об интегралах за тысячелетие до их изобретения. Площади и объемы, бесконечное количество ломтиков, перестановки, которые решают проблему непрерывности и кривизны, – все это химические ингредиенты, «первичный бульон», из которого позднее развились интегралы. Почему же тогда миру так долго пришлось ждать рождения математического анализа?
В тот день римляне взяли город. В течение нескольких часов Сиракузы были сожжены, а солдаты впали в состояние неистовства, грабя и убивая. «Множество жестокостей было совершено сгоряча и из жажды наживы», – писал историк Ливий. Тем не менее римский военачальник Марцелл настаивал на том, чтобы сохранить жизнь великому геометру, «находя в том, чтобы спасти Архимеда, столько же славы, сколько и в разрушении Сиракуз» (по словам другого историка).
Архимед даже не заметил падения города. Что значит какой-то грабеж и разрушения по сравнению с всепоглощающей красотой фигуры на песке?
Историки расходятся во мнении по поводу того, что сказал Архимед, когда к нему приблизился римский солдат. Возможно, он взмолился: «Пожалуйста, не стирайте мои круги!» Может быть, он разбушевался: «Не трогай моих чертежей, парень!» Весьма вероятно, что он прикрыл рисунки ладонями, как будто идеи значили намного больше, чем его собственная жизнь: «Лучше ударьте меня по голове, только не стирайте линии!» В любом случае все источники сходятся в одном: солдат убил Архимеда. Кровь заполнила прочерченные в песке дорожки, оставленные его пальцами. Марцелл настоял на подобающем погребении и осыпал родственников ученого подарками и милостями. Но виновник «бесчисленных бед» был мертв.
Сегодня величайшим наследием Архимеда считаются не катапульты и когти, а геометрия. Его понятные аргументы, его восприятие бесконечности, то, как близко он подошел к математическому анализу. Мог ли один легкий дополнительный толчок привести к нему? Мог ли матанализ возникнуть на Земле на тысячу лет раньше, чем это произошло в реальности?
Обдумайте высказывание математика Альфреда Норта Уайтхеда:
Гибель Архимеда от рук римского солдата – символ перемен первой величины в масштабе всего мира. Греки с их любовью к абстрактной науке уступили лидерство в европейском мире практичным римлянам.
В практичности в целом ничего плохого нет. Или все-таки есть. Премьер-министр Великобритании XIX в. Бенджамин Дизраэли определял практичного человека как «практикующего ошибки своих предков». Согласно Уайтхеду, именно это и делали римляне. Нигде в победившей стране вы не смогли бы найти искру воображения, которая была у побежденных.
Все их усовершенствования состояли в мелких технических деталях. Они не были мечтателями в достаточной степени… Ни один римлянин не поплатился жизнью за то, что был поглощен созерцанием математического чертежа.
Столетия спустя, когда жители Сиракуз забыли о наследии Архимеда, писатель Цицерон предпринял попытки отыскать его могилу. Он нашел ее, «скрытую кустами ежевики и терновника»: «маленькую колонну, едва видневшуюся над зарослями». Цицерон узнал могилу по тому, что было вырезано на ней, как и просил Архимед: сфера и цилиндр. Могила давно исчезла, но она запечатлелась в нашем коллективном воображении, которое может пережить пыль, кровь и все каменные строения, созданные руками римлян.
XXV
Из невидимых сфер
Мир «Флатландии» – романа о многих измерениях
[56] – понятен из его названия. Место действия этого произведения, написанного в 1884 г., является абсолютно плоским: оно более плоское, чем блин, чем лист бумаги, чем женские характеры в фильмах Майкла Бэя. Это мир двух измерений, где имеются длина и ширина, но нет высоты. Тем не менее его обитатели – треугольники, квадраты, пятиугольники и так далее – не ощущают отсутствие одного измерения. На самом деле они, как канзасцы в Канзасе и техасцы в Техасе, не могут представить существование вне своего мира.










