
План Б. Начальная заработная плата снова составляет 10 тысяч фунтов в год, но повышение происходит только в конце года. Заработная плата за первый год равна 10 тысячам фунтов, стало быть, план Б уже менее интересен, чем план А. Крупное повышение заработной платы на 2000 фунтов прибавляется к заработной плате следующего года, и в конце второго года она составит 12 000 фунтов.

Итак, план А по-прежнему лидирует; то же самое будет происходить и на протяжении всех последующих лет. Суммарный эффект более мелких, чаще повторяющихся повышений превосходит крупное повышение один раз в год.
72. ДЕЛЕНИЕ ТРОСТИ
При условии случайного выбора места деления трости на две части любая точка на ней может быть выбрана с равной вероятностью.
В половине случаев эта точка будет находиться на левой половине трости и в половине на правой. (Мы можем исключить из рассмотрения случай, когда она находится посредине, поскольку тогда трость будет поделена на две равные части и, соответственно, меньшей части не будет.)
Что, если трость распилена с левой стороны? Меньшая ее часть будет находиться слева, и этот отрезок попадет в пределы от ноля до половины длины трости. В действительности, так как все точки на меньшем отрезке трости можно выбрать в качестве точки деления с равной вероятностью, длина меньшей части будет в среднем составлять половину длины половины трости, то есть четверть всей ее длины. Если точка деления попадает на правую половину трости, рассуждать следует аналогично. Следовательно, длина наименьшего отрезка трости – в среднем четверть ее общей длины.
73. РУКОПОЖАТИЯ
На званом ужине присутствуют десять человек: Эдвард, Люси и четыре супружеские пары. Следовательно, каждый может пожать руки максимум девяти человекам – всем, кроме себя самого.
Однако в задаче сказано, что никто не пожимает руку знакомому человеку. Можно предположить, что каждый гость знает своего супруга (супругу), а значит, максимальное количество людей, которым один человек может пожать руки, равно восьми.
Эдвард получил девять разных ответов: 0, 1, 2, 3, 4, 5, 6, 7 и 8.
Рассмотрим ответ того, кто назвал число 8. Этот человек пожал руки всем, кроме своего супруга (супруги). Следовательно, каждый человек, за исключением его супруга (супруги), пожал руку как минимум одному человеку. Соответственно, тот, кто назвал число 0, должен быть в паре с тем, кто назвал число 8.
Аналогичным образом проанализируем ответ «7». Этот человек пожал руки всем, кроме своего супруга (супруги) и человека, назвавшего число 0. Значит, все остальные пожали руки как минимум двоим: тому, кто назвал число 8, и тому, кто дал ответ 7. Получается, супруг (супруга) человека, назвавшего число 7, должен был дать ответ 1.
Продолжив рассуждать подобным образом, мы придем к выводу, что третья пара состоит из 6 и 2, а четвертая – из 5 и 3. Осталась только Люси, а она пожала руки четверым.
74. РУКОПОЖАТИЯ И ПОЦЕЛУИ
Начнем с рукопожатий. Все мужчины пожимают друг другу руки. Следовательно, если только один гость – мужчина, то будет всего одно рукопожатие – между ним и Эдвардом. Если среди гостей двое мужчин, будет три рукопожатия: между самими мужчинами из числа гостей, а также между Эдвардом и каждым гостем. А если на ужине четверо гостей мужского пола, рукопожатий будет шесть. Предоставляю вам самим разобраться, кто обменяется рукопожатиями в этом случае.
Итак, нам известно, что три гостя – мужчины.
Женщины целуют всех, кроме своих супругов. Мы знаем, что три гостя – мужчины, значит, у нас уже есть три поцелуя: между Люси и каждым из этих мужчин. Всего двенадцать поцелуев. На скольких гостей пришлись оставшиеся девять поцелуев?
Рассмотрим одну новую гостью – Анну. Если она не замужем, то поцелует Эдварда, Люси и троих мужчин (всего пять поцелуев), если в браке с одним из мужчин, то поцелует только четырех человек. Мы все еще весьма далеки от девяти поцелуев, поэтому подключим еще одну гостью – Беатрис.
Если Беатрис поцелует всех, она поцелует шесть человек. Но если она замужем, поцелуев будет только пять. Могут ли поцелуи Анны и Беатрис дать в сумме девять поцелуев? Да, если обе женщины состоят в браке, поскольку тогда мы насчитаем четыре и пять поцелуев. Мы нашли решение. На ужине присутствовало пять гостей: две пары и один холостяк.
75. ПОТЕРЯННЫЙ БИЛЕТ
Эта головоломка не такая сложная, как кажется. Решение не требует никаких вычислений или уравнений. Единственная трудность – в выборе подхода, но как только вы его найдете, он окажется изящным и простым.
Итак, 100 человек занимают свои места в театральном зале. Проанализируем ситуацию. Чтобы не запутаться, назовем первого человека в очереди A, а последнего Z. Таким образом, мы можем сформулировать вопрос: какова вероятность того, что Z займет свое место, если A сядет на место, выбранное случайным образом?
На рисунке все места расположены в ряд и обозначены буквами от A до Z, то есть место A… место Z.
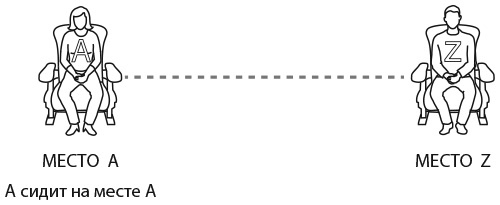
Допустим, посетитель A занял либо место A, либо место Z. Если он сядет на место A, все остальные посетители театра также займут правильные места, в том числе и Z. (Так и было бы, если бы A не потерял билет.)
Если же A займет место Z, то, очевидно, Z не займет свое место, поскольку его уже занял A. В этом случае Z сядет на место A.
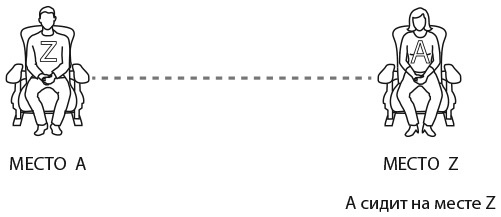
В задаче сказано, что посетитель A выбирает место случайным образом, а значит, он с равной вероятностью может занять как место A, так и место Z. Если ограничиться в ходе рассуждений только этими двумя местами, то Z займет свое место с вероятностью 50: 50.
А что, если A займет любое другое место. Предположим, место посетителя N, который занимает n-е место в очереди.
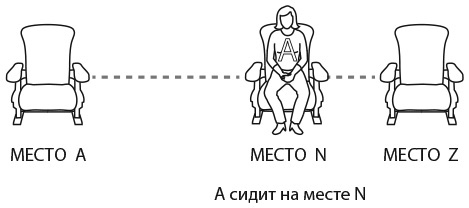
Если A сидит на месте N, то все люди, которые стоят в очереди до N, займут места, указанные в их билетах. Первым, кто не сядет на свое место, будет N, поскольку его место уже занял A. В итоге N выберет одно из оставшихся мест.







