Вариант В. Левая чаша поднимается. В таком случае фальшивая монета должна быть среди монет 1, 2, 3, 4 и 5, а значит, мы можем исключить 6, 7 и 8 из рассмотрения.
Если одна из монет 1, 2, 3, 4 фальшивая, она должна быть тяжелее остальных, поскольку чаша весов с монетами 1, 2, 3, 4 опустилась при первом взвешивании. Следовательно, фальшивой должна быть либо монета 3, либо монета 4. Сравните их вес при третьем взвешивании.
Вариант С. Правая чаша поднимается. Как и в варианте В, фальшивой должна быть одна из этих пяти монет, поэтому мы можем исключить из рассмотрения монеты 6, 7 и 8. И, как и в варианте В, если одна из монет 1, 2, 3, 4 фальшивая, она должна быть тяжелее остальных, потому что чаша весов с монетами 1, 2, 3, 4 опустилась при первом взвешивании. Следовательно, фальшивой может быть монета 1 или 2.
Но остается еще одна возможность. Поскольку чаша весов с монетами 5, 6, 7 и 8 поднялась при первом взвешивании, монета 5 могла бы быть фальшивой и более легкой.
Таким образом, во время последнего взвешивания необходимо сравнить вес монет 1 и 2. Фальшивой будет та, которая лежит в опустившейся чаше, поскольку если чаши весов уравновешены, то правонарушительница – монета 5.
Если после первого взвешивания чаша весов с монетами 1, 2, 3, 4 окажется выше чаши с монетами 5, 6, 7, 8, следует повторить описанные выше действия, поменяв местами монеты 1, 2, 3, 4 и 5, 6, 7, 8.
64. СТОПКА ФАЛЬШИВЫХ МОНЕТ
Разумеется, одно взвешивание!
Положите на весы одну монету из первой стопки, две из второй, три из третьей, четыре из четвертой и так далее до тех пор, пока не выложите десять монет из последней стопки. На весах будет 1 + 2 + 3 + 4 + … + 10 = 55 монет.
Поскольку вам известен вес одной монеты, то вы знаете и общий вес 55 монет. Разность в граммах между весом на весах и весом 55 монет – и есть номер стопки с фальшивыми монетами. Если эта разность составляет 1 грамм, на весах всего одна фальшивая монета и лежит она в первой стопке; если разность составляет 2 грамма, то на весах две фальшивые монеты, а стопка с фальшивыми монетами – вторая, и т. д.
65. ИЗ ГАВРА В НЬЮ-ЙОРК
Впервые узнав об этой головоломке, я сразу же подумал, что ответ – 7; такой же ответ дали и те выдающиеся французские математики, которым эту задачу задал Эдуард Люка.
Путь через океан занимает семь дней. Следовательно, семь лайнеров, которые вы встретите на своем пути, отправятся из Нью-Йорка сегодня, завтра и в следующие дни до тех пор, пока не отправится лайнер в день накануне вашего прибытия.
Но это неправильный ответ! А как же те лайнеры, что отправились из Нью-Йорка на прошлой неделе? Они плывут сейчас в открытом море, и вы, конечно, тоже встретите их. Правильный ответ: в момент отплытия из Гавра вы встретите первый лайнер в порту (этот корабль, отправившийся из Нью-Йорка неделю назад, прибудет в полдень), еще 13 лайнеров в открытом море и последний корабль в Нью-Йорке, откуда он отправится в тот момент, когда вы туда прибудете в полдень через неделю. Все это хорошо видно на рисунке.
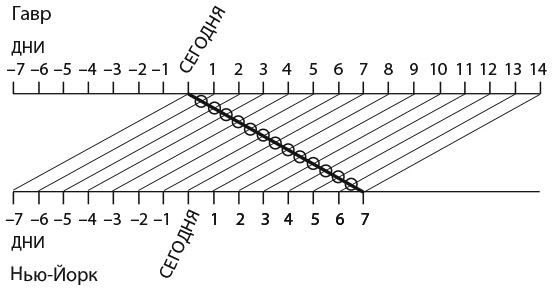
Если все океанские лайнеры перемещаются с постоянной скоростью, вы будете встречать один лайнер каждые 12 часов – один раз в полдень (по времени Гавра) и один раз в полночь.
66. ПОЛЕТ ТУДА И ОБРАТНО
Допустим, ветер дует в направлении движения самолета из пункта А в пункт Б и против движения самолета на обратном пути.
Создается впечатление, что ускорение попутного ветра и сопротивление встречного должны уравновесить друг друга, поскольку скорость, которую придает самолету попутный ветер в одном направлении, нейтрализует ветер на обратном пути. Если скорость ветра равна W, то скорость самолета на пути из пункта А в пункт Б увеличивается на W, а на обратном пути снижается на W.
Однако здесь важна не скорость, а продолжительность полета. Времени, сэкономленного за счет более быстрого полета, меньше, чем времени, потерянного из-за сопротивления ветру, потому что с более низкой скоростью самолет летит дольше.
Мы можем понять это, подставив несколько чисел. Самолет, летящий со скоростью 500 миль в час, пролетает 500 миль за один час. Если он преодолевает то же расстояние со скоростью, на 100 миль в час большей, ему понадобится на 10 минут меньше времени. (Время = расстояние ÷ скорость. Следовательно, если расстояние составляет 500 миль, а скорость – 600 миль в час, то есть 10 миль в минуту, то продолжительность полета в минутах составит 500 ÷ 10 = 50 минут.)
Если скорость самолета на 100 миль в час меньше, то его полет будет на 15 минут дольше. (Если расстояние 500 миль, а скорость 400 миль в час, то продолжительность путешествия в часах равна 500 ÷ 400 = 1,25, или один час с четвертью.)
Таким образом, полет на расстояние 500 миль туда и обратно при скорости ветра 100 миль в час занял бы в целом на пять минут больше времени, чем при полном отсутствии ветра.
Однако даже без всех этих вычислений представьте, что произошло бы, если бы скорость ветра была равна скорости самолета. Самолет преодолел бы путь из пункта А в пункт Б за половину времени. Но на обратном пути его скорость равнялась бы нулю, и он даже не оторвался бы от взлетной полосы!
Конечно, это крайний случай, но он показывает закономерность. Повышая скорость на определенную величину, вы не сможете сэкономить больше времени, чем время полета, а вот снижая скорость на такую величину, можете потерять целую жизнь. Таким образом, если ветер дует в направлении движения самолета, то полет в два конца займет больше времени, чем при полном отсутствии ветра.
А что же боковой ветер? Он может дуть как по курсу движения самолета (или против него), так и перпендикулярно его движению. Поскольку мы знаем, что в первом случае продолжительность маршрута в оба конца увеличивается, что мы можем сказать о втором сценарии? Для того чтобы пролететь по прямой из пункта А в пункт Б при боковом ветре, дующем перпендикулярно, пилоту необходимо вести самолет под углом к направлению ветра, а значит, часть скорости будет потрачена на преодоление ветра, а не на перемещение из пункта А в пункт Б. Так что путешествие туда и обратно тоже займет больше времени.
Лучший сценарий для полета в оба конца – полное отсутствие ветра.
67. ЗАДАЧА О ПРОБЕГЕ АВТОМОБИЛЯ
Прежде всего нужно понять, что первые четыре цифры одометра станут одинаковыми после того, как автомобиль проедет тысячу миль, а счетчик пробега за одну поездку обнулится. К этому моменту он проделает 876,6 мили, которые мы получим, вычислив разность 1000 – 123,4, и приборная панель будет выглядеть так:

Еще через 130 миль станут одинаковыми первые две цифры.




