Сначала умножим уравнение [2] на 6, чтобы избавиться от дробей.
[3] 12 x + 3 y + 2 z = 600.
Кроме того, умножим уравнение [1] на 2, чтобы в нем было 2 z.
[4] 2 x + 2 y + 2 z = 200.
Теперь нам осталось только записать одно уравнение, сократив член 2 z. Преобразовав уравнение [3], получим 2 z = 600 – 12 x – 3 y, а подстановка этого выражения в уравнение [4] даст следующее:
2 x + 2 y + 600 – 12 x – 3 y = 200.
Это уравнение можно привести к такому виду:
[5] 10 x + y = 400.
Нам известно, что x y – целые числа меньше 100. Кроме того, мы можем сделать вывод в отношении y: значение этой переменной должно быть кратным 10. Поскольку 400 делится на 10, другая сторона уравнения 10 x + y тоже должна делиться на 10. Мы также знаем, что 10 x делится на 10, а значит, значение y также должно быть кратным 10, иначе 10 x + y не делилось бы на 10, а это противоречит тому, что нам известно.
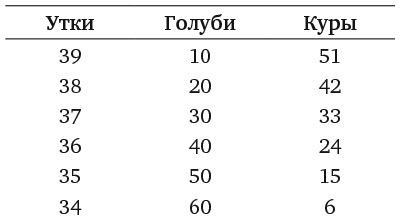
Числа меньше 100, кратные 10, – это 10, 20, 30, 40, 50, 60, 70, 80 и 90. Однако y не может иметь значение 70, 80 или 90, потому что тогда значение x было бы 33, 32 и 31, а сумма x и y превысила бы 100. Шесть искомых решений выглядят так: y = 10, 20, 30, 40, 50 и 60, что дает нам следующее распределение птиц:
53. 7-ELEVEN
Нам необходимо найти цену четырех товаров, но из условия задачи мы знаем только сумму и произведение их цен.
Давайте запишем уравнения. Пусть цены товаров – a, b, c и d. Кассир говорит, что:
[1] a × b × c × d = abcd = 7,11;
[2] a + b + c + d = 7,11.
Согласно основной теореме арифметики, каждое целое число равно произведению уникального множества простых чисел. Эта теорема будет весьма полезна, но мы пока не можем ее применить, поскольку она касается целых чисел, а произведение [1] – дробное число. Наша задача – превратить уравнение [1] в уравнение с целыми числами, что мы сделаем посредством следующих подстановок.
Пусть A = 100 a, B = 100 b, C = 100 c и D = 100 d. Умножив эти значения, получим:
[3] A × B × C × D = ABCD = 100 000 000 abcd.
Но мы знаем, что abcd = 7,11. Значит:
[4] ABCD = 711 000 000.
Теперь у нас есть число, с которым мы можем работать. Основная теорема арифметики говорит нам, что произведение уникального набора простых множителей, то есть простых чисел, равно числу 711 000 000. Эти множители можно найти вручную или, что предпочтительнее, с помощью компьютера:
711 000 000 = 2 × 2 × 2 × 2 × 2 × 2 × 3 × 3 × 5 × 5 × 5 × 5 × 5 × 5 × 79.
Значит, ABCD = 2 × 2 × 2 × 2 × 2 × 2 × 3 × 3 × 5 × 5 × 5 × 5 × 5 × 5 × 79.
Таким образом, числа A, B, C, D состоят из простых чисел. Вопрос в том, как определить, произведение каких чисел дает значение A, произведение каких чисел равно значению B, произведение каких чисел образует C и произведение каких чисел равно D. Другими словами, как соотнести эти числа со значениями A, B, C, D?
Теперь вернемся к уравнению [2] и умножим его на 100, чтобы получить второе уравнение с A, B, C, D:
[5] 100a + 100b + 100c + 100d = A + B + C + D = 711.
То есть мы должны распределить приведенные выше простые числа между A, B, C и D так, чтобы их сумма составляла 711.
Плохо, что здесь нет короткого пути, – необходимо просто применить метод проб и ошибок. Предположим, например, что A = 2 × 2 × 2 × 2 × 2 × 2 = 64, B = 3 × 3 = 9, C = 5 × 5 × 5 × 5 × 5 × 5 = 15 625 и D = 79. В таком случае A + B + C + D = 15 777, а значит, мы сделали неправильный выбор.
Теперь решение задачи во многом зависит от удачи, но постепенно вы начнете понимать, какими именно должны быть значения A, B, C, D. Кроме того, вы можете сделать ряд предположений. У нас много пятерок, следовательно, два или три числа могут быть кратными пяти. В таком случае их сумма будет заканчиваться цифрой 0 или 5, а последнее число должно заканчиваться цифрой 6 или 1. Какое наименьшее кратное числа 79 заканчивается цифрой 6 или 1? Это 79 × 4 и, конечно же:
A = 79 × 2 × 2 = 316;
B = 5 × 5 × 5 = 125;
C = 5 × 3 × 2 × 2 × 2 = 120;
D = 5 × 5 × 3 × 2 = 150.
Таким образом, цены a, b, c, d – это 3,16; 1,25; 1,20; 1,50 фунта.
Красота этой головоломки не в довольно трудоемких операциях, выполненных методом проб и ошибок, а в том, как блестяще число 7,11 обеспечивает единственно возможное решение для каждой из четырех переменных.
54. ТРИ КУВШИНА
Прочитайте решение задачи о бильярдном столе, описанное в разделе головоломки о трех кувшинах.
55. ДВА ВЕДРА
Надеюсь, вы разобрались в задаче о бильярдном столе.
На первом рисунке показано, что произойдет, когда вы сделаете удар кием по шару в точке (7; 0), то есть сначала наполните ведро на 7 галлонов. Второй рисунок соответствует удару кием по шару из точки (0;5), то есть когда вы сначала наполните ведро на 5 галлонов. На первом рисунке шар совершает меньше отскоков, прежде чем попасть в бортик в точке с горизонтальной координатой 6, – так что это способ налить 6 галлонов воды за минимальное количество переливаний.
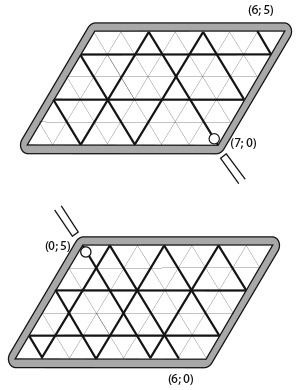
Координаты движения шара на первом рисунке, которые представляют количество галлонов в случае каждого переливания, таковы: (7; 0), (2; 5), (2; 0), (0; 2), (7; 2), (4; 5), (4; 0), (0; 4), (7; 4) и (6; 5). Следовательно, быстрее всего – налить 7 галлонов в первое ведро, оставив второе пустым, затем налить 5 галлонов во второе ведро, оставив в первом ведре 2 галлона, и так далее – до тех пор, пока в первом ведре не окажется 6 галлонов воды, а второе ведро не будет полным.
56. ЗАДАЧА О КОФЕ С МОЛОКОМ




