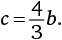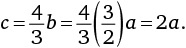Объединив оба уравнения, получим:
πr2 – площадь линз = πr2 – площадь крыльев.
Из этого следует, что площадь линз равна площади крыльев. Поскольку есть четыре крыла равного размера и четыре линзы равного размера, площадь одного крыла равна площади одной линзы.
35. КРУГИ САНГАКУ
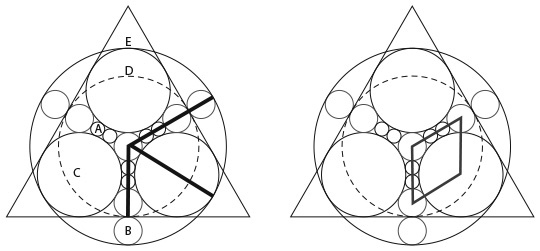
Идеальное совмещение кругов друг с другом на рисунке – не только то, что делает изображение столь привлекательным, но еще и ключ к решению головоломки, так как у нас есть возможность сравнивать радиусы кругов.
Обозначим круги в порядке возрастания размера символами A, B, C, D и E, а их радиусы – a, b, c, d и e. Наша задача – выразить d через a.
На первом рисунке я выделил жирным три отрезка. Вертикальный отрезок – это радиус круга D, обозначенного пунктиром, но этот же отрезок соответствует четырем радиусам круга A и трем радиусам круга B. Следовательно, мы можем записать такое уравнение:
[1] d = 4a + 3b.
Аналогично два других отрезка, радиусы круга E, также можно выразить через радиусы других кругов:
[2] e = 4a + 5b;
[3] e = b + 2c.
Хитрость заключается в том, чтобы понять (благодаря изображению ромба на втором рисунке), что:
[4] 4a + 2b = b + c.
Мы имеем четыре уравнения с пятью неизвестными. Поскольку нам нужно выразить d через a, избавимся от других членов уравнений.
Во-первых, мы можем исключить e, приравняв выражения [2] и [3]:
4a + 5b = b + 2c.
Следовательно,
4a + 4b = 2c, или
[5] 2a + 2b = c.
Подстановка c в уравнение [4] даст такой результат:
4a + 2b = b + 2a +2b, или
[6] 2a = b.
А подстановка в уравнение [1] дает:
d = 4a + 6a = 10a.
Это и есть ответ: радиус круга D в десять раз больше радиуса круга A.
36. ТРЕУГОЛЬНИК САНГАКУ
Я обозначил круги разных размеров символами A, B и C, а их радиусы – a, b и c. Стратегия решения задачи заключается в том, чтобы сначала выразить радиус b через a, а затем c через b, что позволит нам доказать, что с = 2a.
На рисунке я обозначил пунктирной линией треугольник, длина гипотенузы которого равна b + a, поскольку она состоит из радиусов соответствующих кругов, а длина двух других сторон – b и 2b – a. Вторую длину можно вывести исходя из того, что эта сторона треугольника равна половине стороны квадрата, длина которой должна быть равна 4b, за вычетом радиуса круга A.
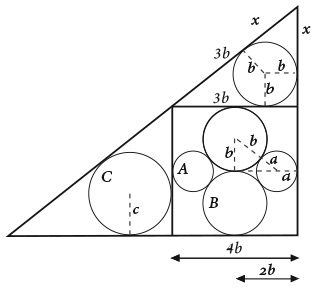
Теорема Пифагора гласит, что во всех прямоугольных треугольниках квадрат гипотенузы равен сумме квадратов катетов, а значит:
(b + a)2 = b2 + (2b – a)2.
Это уравнение можно представить в таком виде:
b2 + 2ab + a2 = b2 + 4b2 – 4ab + a2.
Сократим его до:
6ab = 4b2.
Затем сократим еще раз:
3a = 2b.
И наконец, получим решение:
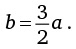
Таким образом, мы выразили b через a.
Теперь посмотрим на верхний треугольник на рисунке. Я построил отрезки от центра круга до каждой из его сторон. Каждый отрезок образует со стороной треугольника прямой угол, а значит, этот треугольник состоит из квадрата b × b и двух фигур в форме воздушного змея. Длинная сторона воздушного змея, смотрящая влево, составляет 3b, поскольку она равна стороне большого квадрата минус радиус круга B. А исходя из того, что воздушные змеи симметричны, вторая сторона змея также должна быть 3b. Если обозначить символом x сторону воздушного змея, смотрящую направо, то с помощью теоремы Пифагора получим:
(3b + x)2 = (b + x)2 + (4b)2.
Раскрыв скобки в уравнении, будем иметь:
9b2 + 6bx + x2 = b2 + 2bx + x2 + 16b2.
Сокращение даст нам следующий результат:
4bx = 8b2.
Отсюда следует:
x = 2b.
Вертикальная сторона верхнего треугольника равна x + b = 2b + b = 3b. Вертикальная сторона нижнего треугольника равна 4b. Учитывая, что эти два треугольника одинаковой формы (хотя и разных размеров), соотношение их сторон, равное
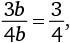 должно быть эквивалентно отношению радиусов кругов, вписанных в эти треугольники, равному b/c.
должно быть эквивалентно отношению радиусов кругов, вписанных в эти треугольники, равному b/c.
Если
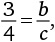 то
то
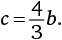
Теперь у нас есть c, выраженное через b, и b, выраженное через a. Следовательно, c можно выразить через a в таком виде:
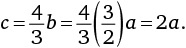





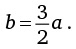
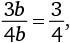 должно быть эквивалентно отношению радиусов кругов, вписанных в эти треугольники, равному b/c.
должно быть эквивалентно отношению радиусов кругов, вписанных в эти треугольники, равному b/c.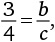 то
то