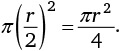
30. НЕЧЕТКАЯ МАТЕМАТИКА
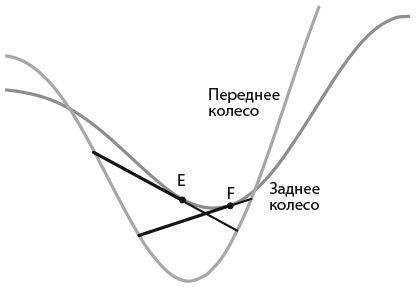
Я обожаю эту головоломку, потому что она иллюстрирует один любопытный феномен: верхняя часть колеса всегда движется быстрее, чем нижняя.
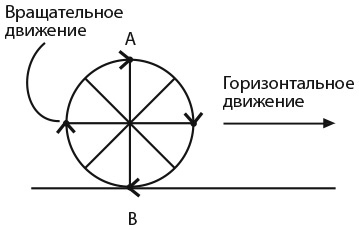
Когда колесо катится по горизонтальной поверхности, все точки на нем совершают движение в двух направлениях: перемещаются горизонтально, в направлении движения, и совершают вращательное движение вокруг центра колеса. Эти два направления движения совмещаются и в определенных случаях нейтрализуют друг друга. Рассмотрим такую точку. Когда она находится сверху (точка A на представленном рисунке), горизонтальное движение дополняет вращательное. Однако когда точка расположена внизу (точка B), вращательное движение направлено в сторону, противоположную горизонтальному, поэтому два движения нейтрализуют друг друга. С позиции наблюдателя точка в верхней части катящегося колеса всегда движется со скоростью, в два раза превышающей горизонтальную скорость колеса, а точка в нижней части колеса всегда неподвижна. Из этого следует, что точки в нижней части колеса перемещаются медленнее, чем в верхней.
Таким образом, ответ на вопрос, поставленный в задаче, – второе изображение, на котором у верхнего пятиугольника размытые очертания, а у нижнего четкие. Это возможно в случае, если выдержка фотоаппарата выставлена на достаточно короткое время, чтобы изображение медленно движущегося пятиугольника получилось четким, а быстро движущегося – расплывчатым. Художник, вероятно, сразу бы это понял, поскольку верхнюю часть движущихся колес всегда рисуют размытой.
31. ХОЖДЕНИЕ ПО КРУГУ
Возможно, вы получили ответ 3 (вариант б) – именно такой ответ экзаменаторы считали правильным.
От учеников они ожидали следующего хода рассуждений. Если радиус круга А равен одной трети радиуса круга В, то длина окружности круга А составляет третью часть длины окружности круга В (так как длина окружности равна произведению 2π на радиус). Следовательно, в одном периметре круга В можно поместить три периметра круга А. Совершая один полный оборот, круг А проходит одну длину окружности. Таким образом, за три полных оборота он пройдет три длины окружности, что равно периметру круга В.

Ошибку экзаменаторов трудно обнаружить, если вы не изучали особенности перемещения круга вокруг других кругов. По всей вероятности, они тоже не изучали эту тему. Давайте сделаем это сейчас. Возьмите две одинаковые монеты и проведите одну вокруг другой. Длина окружности монет одинаковая, а значит, можно было бы ожидать (как указано в задании теста SAT
[40]), что движущаяся монета совершит только один оборот, прежде чем вернется в исходную точку. Тем не менее голова королевы оборачивается дважды! Когда один круг вращается вокруг другого, необходимо прибавить дополнительное вращение с учетом того факта, что этот круг вращается вокруг себя и вокруг второго круга.
Если бы в тесте SAT спрашивалось, сколько раз круг А обернется вокруг своей оси, перемещаясь вдоль отрезка прямой, длина которого равна длине окружности круга В, то ответ был бы – три раза. Но если круг А перемещается вокруг круга В, то правильный ответ – четыре.
Верного решения не было среди возможных вариантов ответов, и это объясняет, почему почти никто не смог решить эту задачу правильно. Обнаружение ошибки повлекло за собой неприятные последствия для экзаменаторов: история появилась на страницах New York Times и Washington Post.
32. ВОСЕМЬ ЧИСТЫХ ЛИСТОВ БУМАГИ
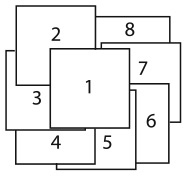
Под листом 1 может находиться только лист, расположенный в левом верхнем углу. А под листом в левом верхнем углу может лежать только лист, расположенный слоем ниже. И так далее по спирали против часовой стрелки.
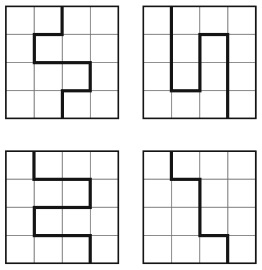
33. КВАДРАТ ИЗ ДВУХ ПОЛОВИНОК
34. КРЫЛО И ЛИНЗА
Задача становится понятнее, если нарисовать полный круг. Разместите четыре одинаковых полукруга таким образом, чтобы получился большой круг с четырьмя пересекающимися кругами меньшего размера.
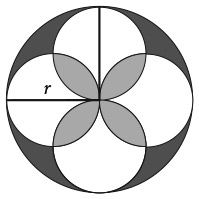
Если r – радиус большого круга, то площадь этого круга – πr2.
Радиус кругов меньшего размера равен половине радиуса большого круга, а значит, площадь каждого малого круга составляет
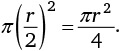
Превосходно! Площадь малого круга равна четвертой части большого круга, следовательно, площадь четырех малых кругов равна площади большого круга. Эквивалентность площадей чрезвычайно полезна, поскольку на нашем рисунке изображены четыре малых круга.
Малые круги перекрывают друг друга. Чему равна общая площадь четырех пересекающихся кругов? Площади четырех малых кругов (πr2) за вычетом площади областей пересечения, то есть площади четырех линз.
1. Площадь пересекающихся кругов = πr2 – площадь линз.
Мы также видим, что площадь пересекающихся кругов равна площади большого круга (πr2) за вычетом площади крыльев.
2. Площадь пересекающихся кругов = πr2 – площадь крыльев.