К этому моменту вы уже получили представление о происходящем. Продолжив ход рассуждений, мы в итоге доберемся до номера автобуса 12.

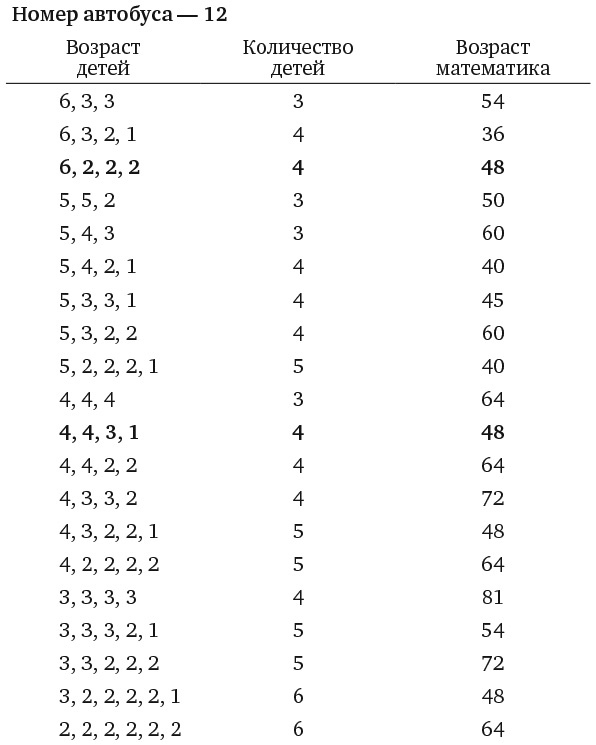
Пришлось немало потрудиться, но мы таки нашли то, что искали. Я выделил эти числа жирным шрифтом.
Даже если бы математик Б знал, что у математика А четверо детей, произведение возрастов которых равно 48, этих данных все равно было бы недостаточно для определения возраста каждого ребенка, потому что это могли бы быть числа 6, 2, 2 и 2 или 4, 4, 3 и 1.
Математик Б знает, что он не может вычислить возраст детей дедуктивным методом, а значит, знает, что математику А должно быть 48 лет.
И нам известно, что номер автобуса – 12.
В описании задачи я отметил, что существует только один возможный номер автобуса, и теперь, после того как мы его установили, задача решена. Однако вы, возможно, захотите получить доказательство того, что номер автобуса не может быть числом 13 или большим. Я не привожу здесь это доказательство, потому что оно слишком сложное для книги такого уровня. Любознательные читатели могут найти его в интернете.
25. ИГРА С ГЛАСНЫМИ
Ответ: нужно перевернуть карточку с буквой A и карточку с числом 2.
Очевидно, что следует перевернуть карточку с буквой A, чтобы проверить, есть ли на обратной стороне нечетное число. Карточку Б переворачивать не нужно, потому что согласные нас не интересуют.
Большинство людей совершают ошибку, полагая, что нужно перевернуть карточку с цифрой 1, чтобы проверить, есть ли на обратной стороне гласная, поскольку 1 – нечетное число. Однако это ошибочная логика. Если на обратной стороне гласная, правило подтверждается. Если же на обратной стороне окажется согласная – не имеет значения, какое число находится на лицевой стороне, так как правило не касается согласных.
Нам необходимо перевернуть карточку с цифрой 2, чтобы убедиться, что на обратной стороне нет гласной, потому что в таком случае правило было бы нарушено.
Психолог Питер Уэйсон придумал эту головоломку в 1966 году. Большинство людей неправильно ее решают не потому, что не понимают вопроса. Скорее всего, они попадают в ловушку рассуждений на основании известных им данных (нечетное число на лицевой стороне), вместо того чтобы исходить из того, что им неизвестно, то есть что находится на скрытой от них стороне. Наш ленивый мозг не создан для решения логических задач!
Однако если сформулировать эту головоломку несколько иначе, включив в нее знакомый социальный контекст, большинство людей находят правильное решение. На изображенных ниже карточках с одной стороны написаны названия напитков, а с другой – числа. Каждая карточка соответствует человеку, причем число обозначает его возраст, а слово – его напиток.
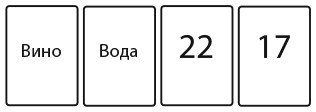
Какие карточки нужно перевернуть, чтобы проверить следующее правило: «Если человек пьет алкоголь, значит, ему больше 18 лет»?
Понятно, что нужно перевернуть карточку с надписью «вино». Однако гораздо очевиднее, что следует перевернуть карточку с числом 17, чтобы узнать, что пьет этот человек. Не нужно выяснять, что пьет 22-летний, поскольку он может пить то, что пожелает.
10 УВЛЕКАТЕЛЬНЫХ ГОЛОВОЛОМОК
УМЕЕТЕ ЛИ ВЫ ИГРАТЬ В СЛОВА?
1. ЛОКО (одно из возможных условий сделки купли-продажи), ОКОТ, ОКОП.
2. ОДНО СЛОВО. Итак, требуется составить словосочетание «одно слово», что и получается из предложенного набора букв.
3. С четырех согласных начинается около тридцати слов, среди них ВЗГЛЯД и ВСКРИК (все остальные подобные слова также начинаются с «вз» или «вс»). Заканчивается четырьмя согласными только одно слово – МОНСТР.
4. Май, Июнь, Июль, Август, Сентябрь, Октябрь, Ноябрь, Декабрь, Январь, Февраль, Март, Апрель.
5. Тригонометрия = ТРИ-Г-ономе-ТРИ-Я
6. Антилопа, автомат, абрикосы.
7. 1) МИГ – маг – май – чай – ЧАС – чад – гад – ГОД – род – рок – бок – бек – ВЕК – бек – бок – боа – бра – ЭРА.
Или после ГОД – гид – вид – вис – вес – ВЕК…
2) МИГ – мир – мор – бор – боа – бра – ЭРА.
8. У Дженнифер в этой системе будет значение 15. Каждый слог в имени дает по 5 очков. Так как в имени Дженнифер три слога, то значение равно 15.
9. Буква о. Если последовательность состоит из семи букв, всегда думайте о днях недели: понедельник, вторник, среда, четверг, пятница, суббота, воскресенье.
10. 1) Хочешь жить – умей вертеться.
2) Продать кота в мешке.
Глава 2. Человек обходит атом. Геометрические задачи
26. ТОЛЬКО ЛИНЕЙКА
Линейка позволяет рисовать прямые линии. Линейкой с расстоянием между делениями в 2 единицы можно рисовать прямые линии и отмечать отрезки длиной 2 единицы. Это все, с чем нам предстоит работать, и этого достаточно.
Наше решение основано на правиле, что две прямые, исходящие из одной точки, расходятся с постоянной скоростью. Нам необходимо найти способ измерить расстояние между двумя расходящимися прямыми, которое позволит нам построить отрезок прямой длиной в 1 единицу. Вот как мы это сделаем.
Шаг 1. Нарисуйте две пересекающиеся прямые. Это и есть расходящиеся прямые. Отметьте на них точки, расположенные ниже точки пересечения на расстоянии двух единиц. Теперь отметьте точки ниже новых точек на расстоянии двух единиц.
Шаг 2. Соедините отрезками первые две точки, а затем вторые. Вы получили два параллельных отрезка. На нижнем отрезке отметьте точку X на расстоянии двух единиц.
Шаг 3. Проведите прямую линию от точки пересечения исходных прямых до точки X. Отметьте точку Y в том месте, где эта прямая пересекается с верхним параллельным отрезком. Расстояние вдоль этого отрезка до точки Y, отмеченное на рисунке жирной линией, равно 1 единице. Мы выполнили задание.
Почему этот способ работает? Я обозначил одну из исходных прямых A, а последнюю проведенную нами прямую – B. Расстояние от прямой A до прямой B в точке пересечения равно нулю. По мере постепенного перемещения вниз по прямой B расстояние от A до B по длине любого отрезка, расположенного под определенным углом, увеличивается с постоянной скоростью. Следовательно, если отрезок AB в точке X имеет длину в две единицы, то параллельный отрезок AB в точке Y, расположенный на полпути к нему, должен быть равен одной единице
[39].





