4. И наконец, проделайте то же самое так, чтобы осталось два равносторонних треугольника.
А теперь пойдем в противоположном направлении и увеличим количество треугольников. Мне очень нравится эта задача, потому что в ней совсем мало спичек.
91. УВЕЛИЧЕНИЕ КОЛИЧЕСТВА ТРЕУГОЛЬНИКОВ
1. Перед вами два треугольника, составленных из шести спичек. Можете ли вы передвинуть две спички на другие места так, чтобы получилось четыре треугольника? Спички разрешается накладывать друг на друга.
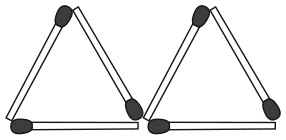
2. Теперь составьте четыре треугольника из шести спичек, не накладывая их друг на друга.
В одной из представленных выше головоломок нужно было разместить пять монет так, чтобы каждая монета соприкасалась со всеми остальными. Предлагаю вам ее другую версию – со спичками.
92. СОПРИКАСАЮЩИЕСЯ СПИЧКИ
В вашем распоряжении по-прежнему шесть спичек. Разложите их так, чтобы каждая спичка соприкасалась со всеми остальными. А теперь найдите способ сделать то же самое с семью спичками.
Расположение спичек, при котором они соприкасаются друг с другом только своими концами, можно воспринимать двумя способами: во-первых, как расположение спичек в определенном порядке, а во-вторых, как сеть точек, соединенных спичками, как показано в следующей головоломке.
93. СОЕДИНЕНИЕ ТОЧЕК
Найдите такое расположение двенадцати спичек, при котором оба конца каждой спички соприкасаются с концами двух других спичек. Иначе говоря, составьте сеть точек, соединенных спичками, в которой каждая точка связана с тремя другими.
В завершение игр со спичками давайте проанализируем следующий неожиданный аспект этой темы, на который обратил внимание наш старый друг Генри Дьюдени.
94. ДВЕ ОГРАДЫ
На рисунке изображено 20 спичек, из которых построены две прямоугольные ограды, состоящие из 6 и 14 спичек соответственно. Площадь второго прямоугольника в три раза больше площади первого.
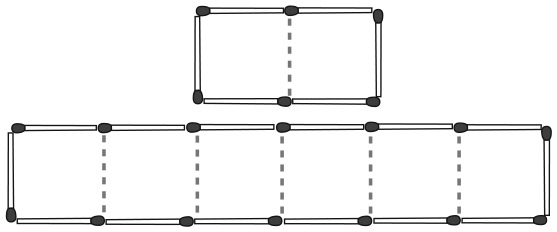
Переместите одну спичку из большей ограды в меньшую таким образом, чтобы получилось две группы по 7 и 13 спичек. Можете ли вы построить две новые ограды так, чтобы площадь второго огражденного участка по-прежнему в три раза превышала площадь первого участка?
Когда я читаю книги Дьюдени, меня неизменно поражает его способность находить блестящий материал для головоломок с использованием самых разных предметов, которые можно найти в кармане. Ниже представлена замечательная головоломка, в которой используется блок из восьми марок. Если у вас нет марок, возьмите лист бумаги и разделить его сгибами так, как показано на рисунке.
В любом случае пришло время взять в руки ножницы, поскольку они понадобятся вам для решения оставшихся головоломок.
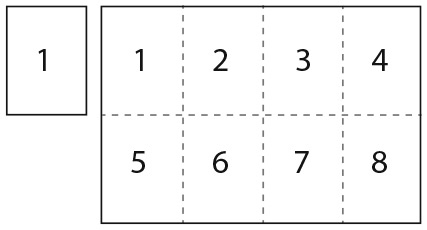
95. СКЛАДЫВАНИЕ МАРОК
На рисунке изображен блок марок, в котором они пронумерованы от 1 до 8. Вам нужно сложить их по линиям сгиба так, чтобы марка с номером 1 была расположена лицевой стороной вверх, а все остальные находились под ней.
Можете ли вы сложить марки так, чтобы они располагались в последовательности 1, 5, 6, 4, 8, 7, 3, 2 и (более трудная задача) 1, 3, 7, 5, 6, 8, 4, 2?
«Это очень интересная задача, – убеждал Дьюдени. – Не откладывайте ее в сторону, если сочтете неразрешимой!»
Дьюдени также придумал следующую задачу с использованием блока квадратных марок.
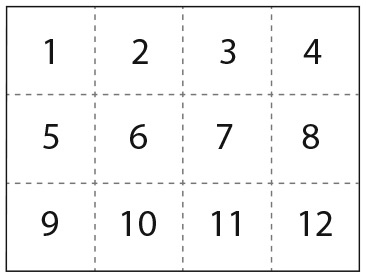
96. 4 МАРКИ
У вас есть набор из 12 квадратных марок в виде блока 3 × 4, как показано на рисунке. Ваш друг просит дать ему четыре марки. Вы решаете оторвать четыре марки, соединенные вместе, – например, номера 1, 2, 3, 4, или 1, 2, 5, 6, или 1, 2, 3, 6, или 1, 2, 3, 7 и т. д. Но есть одно условие: марки не могут крепиться между собой углами, но могут соединяться с другими марками любой стороной.
Сколько существует возможных наборов из четырех марок, соединенных друг с другом?
В ответе на эту задачу в конце книги я нарисовал все возможные фигуры, которые можно составить из соединенных марок. Взгляните на эти рисунки после того, как решите головоломку. Вам они знакомы?
Да, в головоломке Генри Дьюдени есть группа фигур, известных как блоки игры «Тетрис».
Для тех немногих из вас, кто никогда не играл в эту игру, скажу: это очень простая, невероятно увлекательная компьютерная игра, в которой блоки из четырех соединенных квадратов (таких как на рисунке в решении головоломки) выпадают из верхней части экрана. Игрок должен складывать их, передвигая по горизонтали или поворачивая.
Изобретателя «Тетриса» Алексея Пажитнова вдохновила работа Соломона Голомба – американского математика, который опубликовал книгу о фигурах, составленных из соединенных квадратов, в 1965 году. Источником вдохновения для самого Голомба были работы Дьюдени.
Дьюдени не получил формального образования, но у него была поразительная врожденная способность использовать в головоломках идеи, которые впоследствии многие математики считали заслуживающими научного исследования. В первую книгу Дьюдени, «Кентерберийские головоломки», включена его первая головоломка с фигурами, составленными из соединенных квадратов. Она основана на (не совсем достоверной) истории из книги Джона Хейворда о жизни Вильгельма Завоевателя
[30], увидевшей свет в 1613 году. Сыновья Вильгельма, Генри и Роберт, нанесли визит Луи
[31], наследнику французского престола. Когда Генри выиграл у Луи партию в шахматы, произошла потасовка. «Генри в свою очередь ударил Людовика по голове шахматной доской, в кровь разбив ему лицо, – пишет Хейворд. – Братья тотчас вскочили на коней, и, как уверяют, их шпоры были столь остры, что им удалось добраться до своих владений, хотя французы преследовали их по пятам». О-ля-ля!






