По всей вероятности, вы не слышали о Nikoli, но наверняка знаете о судоку, которые впервые появились в журнале Puzzle Communication Nikoli в середине 1980-х годов. Словом «судоку» в Nikoli назвали головоломку Number Place («Место числа»), опубликованную в американском журнале Dell Pencil Puzzles and Word Games. Если на протяжении прошедшего десятилетия вы жили в пещере, позвольте сообщить, что судоку представляет собой квадрат 9 × 9 клеток с несколькими указанными цифрами. Игрок должен заполнить пустые клетки так, чтобы каждая цифра встречалась в каждой строке, в каждом столбце и в каждом малом квадрате 3 × 3 только один раз. Судоку не пользовались особой популярностью до 1986 года, когда в Nikoli решили размещать заданные цифры симметрично, подобно буквам в кроссворде. Небольшое изменение оказалось эффективным, и головоломка обрела успех в Японии. В конце 2004 года судоку впервые появились на Западе, после того как отставному судье Уэйну Гулду, проводившему отпуск в Японии, попалась на глаза эта головоломка. Гулд разработал компьютерную программу для создания таблиц судоку и продал ее британским газетам, в том числе лондонской Times. Через несколько месяцев после первой публикации судоку в Times головоломку начали ежедневно публиковать многие периодические издания во всем мире.
Есть доля иронии в том, что компания Nikoli обрела известность благодаря головоломке, которую не создавала. Однако с момента выхода ежеквартального журнала Nikoli в нем было опубликовано около 600 новых видов головоломок. Nikoli специализируется на матричных головоломках типа судоку, в которых необходимо заполнять матрицу, обычно в форме квадрата. Внимание к деталям – один из факторов, обеспечивающих к ним интерес: в красивых квадратах судоку элементы расположены симметрично, но даже если симметрии нет, судоку все равно создается с большим вниманием к внешнему виду. Правила всегда очень просты, а постепенное заполнение клеток доставляет огромное удовольствие людям вроде меня и оказывает такое же терапевтическое воздействие, как раскрашивание рисунков. Чтобы пробудить в вас интерес к подобным головоломкам, я выбрал четыре примера.
Тираж журнала, публикуемого Nikoli, – около 50 тысяч экземпляров. Среди его читателей не только любители решать головоломки, но и их создатели, присылающие в редакцию несколько сотен предложений в год. Следующая головоломка – «Прямоугольники» (Shikaku – «разделить на квадраты»); ее идея принадлежит 21-летнему студенту по имени Ёсинао Анпуку. Впоследствии он начал работать в Nikoli и сейчас занимает там должность исполнительного редакционного директора.
46. ПРЯМОУГОЛЬНИКИ
В головоломке «Прямоугольники» нужно разделить матрицу на прямоугольные и квадратные блоки. Числа в ячейках матрицы определяют площадь блока, содержащего это число (оно эквивалентно количеству ячеек в блоке).
Разберем пример. На представленном ниже рисунке A – исходная матрица, а C – решение, в котором отмечены все прямоугольные и квадратные блоки. Вначале необходимо найти наибольшее число в исходной матрице, поскольку зачастую формы и положение блоков с этим числом будут иметь определенные ограничения. Самое большое число в данной головоломке – 9, а единственно возможные блоки для числа 9 – прямоугольник 9 × 1 или квадрат 3 × 3. В этой матрице нет горизонтальных или вертикальных последовательностей из девяти пустых ячеек, поэтому блок числа 9 должен быть квадратом и может располагаться только в одном положении, показанном на рисунке B. Аналогично единственный прямоугольный блок из восьми ячеек, который содержит число 8, а также единственный прямоугольный блок из шести ячеек, содержащий число 6, должны находиться на отмеченных местах. Как только будут отчерчены некоторые блоки, вы сможете определить позиции других блоков.
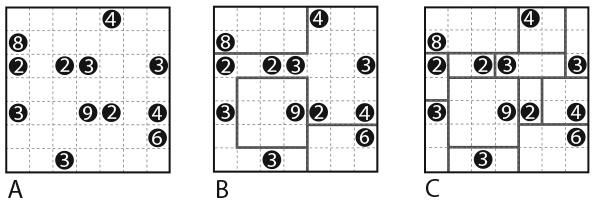
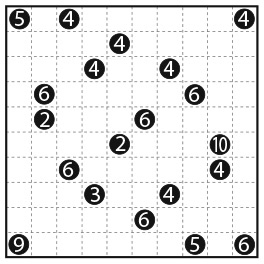
А теперь ваша очередь.
Компанию Nikoli основал Маки Кадзи – страстный любитель скачек, поэтому он назвал ее в честь подготовленного в Ирландии жеребца, который, будучи фаворитом, проиграл на скачках в Эпсоме в 1980 году. Впервые я встретился с Кадзи в 2008-м, в офисе Nikoli в Токио. Он рассказал мне о двух своих хобби – коллекционировании канцелярских резинок и фотографировании номерных знаков, на которых цифры соответствуют строкам таблицы умножения, например: 23 06 (2 × 3 = 6) и 77 49 (7 × 7 = 49). Во время следующей нашей встречи в 2016 году Кадзи сообщил, что его коллекция канцелярских резинок продолжает расти и пополнилась новыми интересными экземплярами из Таиланда и Венгрии. Что касается фотографий номерных знаков, у него уже набралось 85 процентов изображений строк из таблицы умножения от 1 до 9. «Я близок к завершению, – сообщил мне Кадзи, – у меня есть правило: не искать такие номерные знаки намеренно. Я фотографирую только те, которые попадаются случайно».
47. КИТАЙСКАЯ СТЕНА
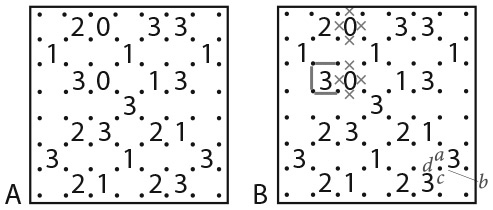
Цель головоломки «Китайская стена» (от англ. slitherlink – скользящие линии) – соединить точки горизонтальными и (или) вертикальными линиями так, чтобы получился один замкнутый контур. Числа в ячейках обозначают количество линий, которые могут быть расположены вокруг соответствующего числа. Так, вокруг ячейки с числом 1 должна проходить только одна линия, вокруг ячейки с числом 2 – две и т. д. Вокруг пустых ячеек можно проводить любое количество линий. Однако полученный контур не должен пересекаться и разветвляться.
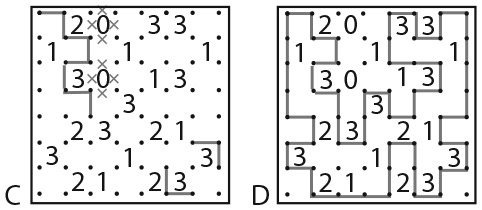
На представленном ниже рисунке A самые очевидные варианты начала – это ячейки с числом 0, поскольку вокруг них не будет линий. Отметьте их маленькими крестиками, чтобы видеть, что там не должно быть никаких линий, как показано на рисунке B. Один из крестиков расположен возле ячейки с цифрой 3, что оставляет место только для трех линий вокруг нее. Нарисуйте их. На рисунке C мы можем продолжить контур вверх, причем существует лишь один способ обвести ячейку с цифрой 2 двумя линиями. Обратите внимание: на рисунке B я отметил также точки a, b, c и d в тех местах, где потенциальные линии могут выйти из точки между ячейками с цифрой 3. Контурная линия должна пройти через эту точку, так как в случае, когда ячейку окружают три линии, они проходят через четыре точки. Контур проводится либо через a, либо через b, либо через c, либо через d, поскольку, если он проходит и через a, и через b или через c и d, образуется ответвление, а это запрещено условием задачи. Во всех случаях контурная линия проводится через две другие стороны обеих ячеек с цифрой 3, поэтому мы можем отметить их на рисунке С. Решение задачи представлено на рисунке D.
Следующую головоломку решите самостоятельно. Помните, что единственный контур должен быть замкнут без пересечений и ответвлений. Существует лишь одно решение, и оно может быть найдено только с помощью логики.






