Бернард: Я все еще не знаю, когда у Дениз день рождения, но знаю, что Шерил тоже не знает.
Шерил: Я все еще не знаю, когда у Дениз день рождения, но знаю, что Альберт пока не знает.
Альберт: Теперь я знаю, когда у Дениз день рождения.
Бернард: Теперь я тоже знаю.
Шерил: И я.
Когда же день рождения у Дениз?
Еще один важный предшественник задач о Шерил – «Невозможная головоломка» голландского математика Ганса Фройденталя, опубликованная в 1969 году; в нее впервые был добавлен диалог «я не знаю – теперь я знаю» из предыдущих задач. В полном соответствии с названием эту головоломку практически невозможно решить с помощью ручки и бумаги, поэтому я не включил ее в эту книгу. (Однако если вы твердо намерены проверить свои силы, поищите ее в интернете.) «Невозможная головоломка» также относится к другому типу логических задач, который восходит как минимум к первой половине прошлого века. В них необходимо дедуктивным методом вывести ряд чисел, зная их сумму и произведение. Как правило, в таких задачах речь идет о возрасте, а героями чаще всего бывают священнослужители.
23. ВОЗРАСТ ДЕТЕЙ
Викарий спросил церковного служителя: «Сколько лет вашим троим детям?»
Служитель ответил: «Сложив их возраст, вы получите номер на моей двери. Умножив их возраст, получите число 36».
Викарий ушел, но, вернувшись через какое-то время, сказал, что не может решить задачу.
Служитель сказал викарию: «Ваш сын старше любого из моих детей» – и прибавил, что теперь викарий сможет решить головоломку.
Определите возраст детей церковного служителя.
Эта задача приводит нас к предпоследней головоломке в этой главе, придуманной британским математиком Джоном Конвеем, почетным профессором Принстонского университета. Последний раз я встретился с ним на междисциплинарной конференции по математике, головоломкам и фокусам. Конвей заявил тремстам участникам, что такие люди, как он, нуждаются в подбадривающем приветствии, и предложил использовать следующий жест: указывая на себя, как можно более слабым голосом произнести слово «нерд»
[13]. Затем он попросил всех присутствующих воспроизвести приветствие нердов. Игривый характер Конвея оказал большое влияние на всю его академическую карьеру: он изобрел много игр и головоломок, самая знаменитая – игра «Жизнь». В ее основе лежит математическая модель эволюции, которую ученые вроде Стивена Хокинга приводят в качестве иллюстрации того, как простые правила могут породить сложное поведение.
Представленная ниже задача Конвея – настоящий шедевр. Она пародирует головоломки, в которых разные факты известны разным людям, и является блестящим примером подобных задач. Как и все лучшие логические задачи со времен Алкуина, эта представляет собой забавную историю, в которой на первый взгляд слишком мало данных для поиска решения.
24. МАТЕМАТИКИ В АВТОБУСЕ
Вчера вечером, сидя в автобусе позади двух математиков, я подслушал их разговор.
А: У меня несколько детей, возраст которых представляет собой натуральные числа. Сумма этих значений равна номеру автобуса, а произведение – моему возрасту.
Б: Как интересно! Возможно, если бы ты сказал мне свой возраст и количество детей, я мог бы определить возраст каждого из них?
А: Нет.
Б: Ага! НАКОНЕЦ-ТО я знаю, сколько тебе лет!
Какой номер автобуса?
Если математик говорит «нет», это не свидетельствует о его ворчливости или пренебрежительности. Просто он имеет в виду, что, если сообщит свой возраст или количество детей, у собеседника все равно будет недостаточно сведений, чтобы определить возраст каждого ребенка.
Чтобы упростить поиск решения, скажу, что у математика больше одного ребенка, но только один малыш в возрасте одного года. И есть лишь один вероятный номер автобуса.
Вперед, за разгадкой!
В заключение, чтобы подготовить вас к решению геометрических задач в следующей главе, позвольте предложить визуальную логическую головоломку.
25. ИГРА С ГЛАСНЫМИ
На рисунке на четырех карточках с одной стороны изображена буква, а с другой цифра.

Какие карточки нужно перевернуть, чтобы проверить истинность следующего утверждения: «На другой стороне всех карточек с гласной изображено нечетное число»?
10 увлекательных головоломок. Умеете ли вы играть в слова?
[14]
1. Добавьте либо в начало, либо в конец приведенной ниже последовательности букв одну букву так, чтобы получилось слово. Составьте не менее трех таких слов.
ОКО
2. Составьте словосочетание из набора букв:
Л О С О Н Д О О В
3. Назовите несколько слов, которые начинаются с четырех согласных. Затем найдите слово, которое оканчивается четырьмя согласными.
4. Иван Иванов работает в компании АСОНД. Вот его визитка:
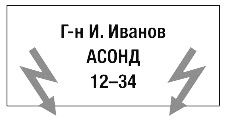
Видите ли вы здесь закономерность?
5. Какое слово начинается с трех букв «г» и заканчивается тремя буквами «я»?
6. (Детская задачка-анаграмма типа «Грамматика + математика = отгадай слово». Чтобы составить анаграмму, нужно переставить буквы в слове и получить новое.) Выполните следующие задания:
Липа + нота = животное
Том + вата = оружие
Рыба + соки = фрукты
7. Как сделать из мухи слона? МУХА – муpа – туpа – таpа – каpа – каpе – кафе – кафp – каюp – каюк – кpюк – уpюк – уpок – сpок – сток – стон – СЛОH. Вот так за 16 ходов «муха» превратилась в «слона». В этих головоломках за один ход можно заменять лишь одну букву, причем порядок следования букв менять нельзя
[15].




