Еще более значимый аспект работы Фурье состоял в том, что он сделал первый шаг к использованию анализа в качестве предсказателя того, как может двигаться и изменяться континуум частиц. Это был огромный шаг вперед по сравнению с трудами Ньютона о движении дискретного множества частиц. За последующие столетия ученые развили методы Фурье и теперь предсказывают поведение других непрерывных сред – например, флаттера на крыле Boeing 787, внешнего вида пациента после лицевой пластики, потока крови по артериям или перемещения земной поверхности после землетрясения. Сегодня эти методы используются в науке и технике повсеместно. Их применяют для изучения ударных волн при термоядерном взрыве; радиоволн для связи; волн в кишечнике, которые помогают усваивать питательные вещества и перемещать продукты жизнедеятельности в нужном направлении; патологических электрических волн в мозге, связанных с эпилепсией и болезнью Паркинсона; а также волн заторов на автострадах с раздражающим явлением фантомных пробок, когда движение замедляется без всяких видимых причин. Идеи Фурье и их различные вариации позволили объяснить все эти явления с математической точки зрения – иногда с помощью формул, иногда путем сложного компьютерного моделирования, так что мы можем объяснить и предсказать эти явления, а в некоторых случаях и управлять ими или устранить их.
Почему синусоиды?
Прежде чем перейти от синусоидальных волн к их двумерным и трехмерным аналогам, давайте выясним, что же делает синусоиды такими особенными. В конце концов, строительными блоками могут быть и другие функции, и иногда они работают лучше синусоидальных волн. Например, чтобы улавливать локальные особенности вроде отпечатков пальцев, ФБР применило вейвлеты. Вейвлеты часто превосходят синусоиды во многих задачах обработки изображений или сигналов – в таких областях, как анализ землетрясений, реставрация или установление подлинности произведений искусства, распознавание лиц.
Так почему же именно синусоидальные волны так хорошо подходят для решения волнового уравнения, уравнения теплопроводности и других дифференциальных уравнений в частных производных? Их преимущество в том, что у них очень специфичные производные. Собственно говоря, производная синусоиды – это та же синусоида, только сдвинутая на четверть цикла. Это замечательное свойство. Оно не выполняется для других типов волн. Как правило, кривая любого рода после дифференцирования изменяется. Ее форма становится другой. Дифференцирование весьма травматический опыт для большинства кривых. Но не для синусоид. После дифференцирования синусоида невозмутимо отряхивается, оставаясь все той же синусоидой. Единственная получаемая ею травма – по сути, и не травма вовсе – это сдвиг волны во времени. Она достигает пика на четверть цикла раньше, чем исходная.
Мы наблюдали несовершенную версию этого явления в главе 4, когда рассматривали увеличение продолжительности светового дня в Нью-Йорке в 2018 году и сравнивали его с ежедневными изменениями продолжительности дня и их скоростью от одних суток к следующим. Мы видели, что обе кривые выглядели примерно синусоидальными, но скорость изменения продолжительности дня создавала волну, сдвинутую на три месяца раньше, чем волна исходных данных. Попросту говоря, самый длинный день в 2018 году был 21 июня, а самое быстрое удлинение дня – на три месяца раньше, 20 марта. Именно этого мы и ожидаем от синусоидальных данных. Если бы данные о длине дня представляли собой идеальную синусоидальную волну и мы бы смотрели на разницу не между сутками, а между соседними моментами, то мгновенная скорость изменений («производная» волна) сама была бы идеальной синусоидой, сдвинутой ровно на четверть цикла. Также из главы 4 мы узнали, почему происходит такой сдвиг на четверть. Это вытекает из глубокой связи между синусоидами и равномерным движением по окружности. (Вы можете вернуться к этим рассуждениям, если сейчас объяснение кажется вам туманным.)
Сдвиг на четверть цикла обладает поразительными следствиями. Это означает, что, взяв две производные, мы дважды сдвинемся на четверть цикла, то есть в общей сложности на половину цикла. А значит, бывший пик превращается во впадину и наоборот. Синусоида перевернулась. В математических терминах это записывается в виде формулы
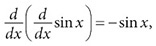
где символ дифференцирования Лейбница d / dx означает «взятие производной от выражения, стоящего справа». Формула показывает, что взять две производные от синуса равнозначно умножению на –1. Такая замена двух производных простым умножением – фантастическое упрощение. Получение второй производной – полноценная операция анализа, в то время как умножение на – 1 – это школьная арифметика.
Но зачем, можете вы спросить, кому-то вообще понадобилось брать эти две производные? Потому что это делает природа, причем постоянно. Вернее, постоянно делают наши модели природы. Например, в ньютоновском законе движения F = ma ускорение a подразумевает две производные. Вспомните, что ускорение – это производная скорости, а скорость – производная расстояния. Следовательно, ускорение – это производная производной расстояния, или, проще говоря, вторая производная расстояния. Вторые производные встречаются в физике и технологии повсеместно. Они присутствуют не только в упомянутом уравнении Ньютона, но и в уравнении теплопроводности и волновом уравнении.
Вот почему синусоидальные волны так хорошо подходят для таких уравнений. Для них вторые производные сводятся к простому умножению на –1. Фактически операции анализа, которые затрудняют изучение уравнения теплопроводности и волнового уравнения, перестают быть проблемами. Анализ пропадает, поскольку заменяется умножением. Именно это значительно упрощает задачи о движении струны и о теплопередаче для синусоидальных волн. Если бы из них можно было сконструировать произвольную кривую, то она унаследовала бы все достоинства синусоид. Единственная загвоздка – для построения произвольной кривой пришлось бы складывать бесконечное количество синусоид, но это небольшая цена.
Это объясняет, почему синусоиды особенные. У физиков тоже есть собственная точка зрения, и ее стоит понять. Для физика самое замечательное в синусоидах (в контексте задач о колебаниях и теплопередаче) то, что они образуют стоячие волны. Они не двигаются вдоль по струне или стержню, а остаются на месте. Они колеблются вверх-вниз, но никогда не распространяются. Еще более примечательно, что стоячие волны колеблются с единственной частотой
[295]. Это редкость в мире волн. Большинство волн – это сочетание многих частот, так же как белый свет – сочетание всех цветов радуги. В этом отношении стоячая волна – это чистая волна, а не смесь.
Визуализация вибраций: фигуры Хладни
Теплый звук гитары и жалобное звучание скрипки связаны с колебаниями, возникающими в деке и корпусе инструмента, в древесине и во внутренних полостях, где звуковые волны колеблются и резонируют. Эти схемы колебаний определяют качество и голос инструмента. Именно это делает творения Страдивари такими особенными – его выразительные уникальные схемы колебаний в древесине и воздухе. Мы до сих пор в точности не знаем, почему одни скрипки звучат лучше других, но ключевым соображением должны быть способы вибрации.