Большая часть истории жизни – рассказ о движении организмов в сторону усложнения, которое строится на предшественниках. Это же справедливо и для математического анализа. Но куда ведет эта история? Есть ли какое-то направление у эволюции анализа? Или она, как некоторые говорят о биологической эволюции, не направлена и случайна?
В рамках чистой математики эволюция анализа была историей скрещивания и его преимуществ. Старые области математики обрели новую жизнь после скрещивания с анализом. Например, давнее изучение чисел и их закономерностей оживилось благодаря появлению инструментов, основанных на анализе, таких как интегралы, бесконечные суммы и степенные ряды. Получившийся гибрид называется аналитической теорией чисел. Аналогичным образом дифференциальная геометрия использовала анализ, чтобы пролить свет на структуру гладких поверхностей, и открыла новые горизонты, о которых даже не подозревала, – невообразимые криволинейные формы в четырех измерениях и выше. В этом смысле «кембрийский взрыв» анализа сделал математику более абстрактной и более мощной, а также придал ей ореол семейственности. Анализ выявил сеть скрытых взаимосвязей, соединяющих воедино все ее части.
В прикладной математике эволюция анализа – это история нашего расширяющегося понимания изменений. Как мы уже видели, анализ начался с изучения кривых, где изменения были изменениями направления, и продолжился изучением движения, когда изменения стали изменениями местоположений. После своего «кембрийского взрыва», и особенно с развитием дифференциальных уравнений, анализ перешел к изучению изменений в более общем смысле. Сегодня дифференциальные уравнения помогают нам предсказывать распространение эпидемий, место появления урагана и сколько платить за опцион на покупку акций в будущем
[259]. Во всех областях человеческой деятельности дифференциальные уравнения стали основой для описания изменений в вещах вокруг и внутри нас, от субатомного уровня до самых дальних уголков космоса.
Логика природы
Самый ранний триумф дифференциальных уравнений изменил ход развития западной культуры. В 1687 году Исаак Ньютон предложил систему мира
[260], которая демонстрировала силу разума и положила начало эпохе Просвещения
[261]. Он открыл несколько уравнений – законы движения и тяготения, – которые смогли объяснить загадочные закономерности, обнаруженные Галилем и Кеплером в падении тел на Земле и в орбитах планет Солнечной системы, и тем самым устранил пропасть между земным и небесным. После Ньютона существовала только одна Вселенная, с одинаковыми законами, действовавшими везде и всегда.
В своем фундаментальном трехтомном шедевре «Математические начала натуральной философии» (чаще называемом просто «Начала») Ньютон применил свои теории к самым разным вещам: форме Земли с ее слегка выпуклой талией, вызванной центробежными силами при вращении; ритму приливов и отливов; эксцентрическим орбитам комет; движению Луны – задаче настолько сложной, что Ньютон даже пожаловался своему другу Эдмунду Галлею, что от нее у него «разболелась голова, и он так часто не мог уснуть, что больше не думал об этом»
[262].
Сегодня при изучении физики студентам сначала преподают классическую механику – механику Ньютона и его последователей, после чего сообщают, что ее вытеснили теория относительности Эйнштейна и квантовая теория Планка, Эйнштейна, Бора, Шрёдингера, Гейзенберга и Дирака. В этом, безусловно, немало правды. Новые теории опровергли представления Ньютона о пространстве и времени, массе и энергии, да и самом детерминизме, заменив его в случае квантовой теории более вероятностным, статистическим описанием природы.
Однако это не изменило роли анализа. И в теории относительности, и в квантовой механике законы природы по-прежнему записываются на языке анализа, с предложениями в виде дифференциальных уравнений. Для меня величайшее наследие Ньютона заключено именно в этом. Он показал, что природа логична. Причина и следствие в мире ведут себя во многом так же, как доказательство в геометрии, когда одна истина вытекает из другой, с той лишь разницей, что в мире одно событие вытекает из другого, а в нашем разуме – одна идея из другой.
Эта сверхъестественная связь между природой и математикой восходит к пифагорейской мечте. Связь между музыкальной гармонией и числами, открытая пифагорейцами, побудила их провозгласить, что всё есть число. В чем-то они были правы. Числа важны для работы Вселенной, собственно, как и формы: в книге природы, о которой мечтал Галилей, слова были геометрическими фигурами. Но какими бы важными ни были числа и фигуры, не они настоящие движущие силы в этой игре. В драме Вселенной формы и числа подобны актерам; их незримо направляет невидимое присутствие и логика дифференциальных уравнений.
Ньютон первым проник в эту логику Вселенной и построил вокруг нее систему. До него это было невозможно из-за отсутствия необходимых понятий. Архимед не был знаком с дифференциальными уравнениями. Не знали их и Галилей, Кеплер, Декарт и Ферма. Лейбниц знал, но не обладал такой склонностью к науке, как Ньютон, и его математической виртуозностью. Тайная логика природы была дарована только Ньютону.
Центральной частью его теории стало дифференциальное уравнение движения:
Это одно из самых важных уравнений в истории. Оно говорит, что сила F, приложенная к телу, равна произведению массы тела m на его ускорение a. Это дифференциальное уравнение, поскольку ускорение является производной (скоростью изменения скорости тела) или, в терминах Лейбница, отношением двух дифференциалов:
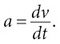
Здесь dv – это бесконечно малое изменение скорости тела v за бесконечно малый интервал времени dt. Таким образом, зная силу F, действующую на тело, и его массу m, мы можем использовать соотношение F = ma для вычисления его ускорения по формуле a = F / m. В свою очередь, это ускорение определяет, как будет двигаться тело. Оно сообщает нам, как будет меняться скорость тела в следующее мгновение, а скорость говорит нам, как изменится положение тела. В этом смысле формула F = ma – это своеобразный оракул. Она предсказывает будущее поведение тела, один крохотный шажок за другим.