Он был беспокойным, одиноким маленьким мальчиком, у которого не было друзей, зато имелась масса свободного времени. Он самостоятельно занимался научными исследованиями, построил на ферме солнечные часы, наблюдая за игрой света и тени на стене. В 1653 году, когда Исааку исполнилось 10 лет, мать снова овдовела и вернулась домой с тремя маленькими детьми – двумя дочерьми и сыном. Она отправила Исаака в школу в Грэнтеме, в восьми милях от дома, – слишком далеко, чтобы ходить туда каждый день пешком. Поэтому мальчик поселился у аптекаря и химика Уильяма Кларка, где познакомился с разными лекарственными препаратами – узнал, как их кипятить, смешивать, растирать пестиком в ступке. Школьный учитель Генри Стокс обучил его латыни, азам теологии, греческому, ивриту, а также некоторым полезным для фермеров расчетам по математике, связанным с геодезией; а кроме того, и более глубоким вещам – например, как Архимед оценил число π. Хотя в школьных документах мальчика характеризовали как бездельника и невнимательного ученика
[209], когда Исаак оставался вечером у себя в комнате один, он рисовал на стенах фигуры – окружности и многоугольники, как у Архимеда.
В шестнадцать лет мать забрала его из школы и заставила управлять семейной фермой. Он ненавидел это занятие; в результате дошло до того, что его свиньи бегали по полям соседей, а заборы развалились, из-за чего местный суд оштрафовал его. Не обошлось и без ссор с матерью и сводными сестрами. Исаак часто уходил в поле, ложился там и читал в одиночестве. Он строил водяные колеса в ручье и наблюдал, какие вихри они создают в потоке.
Наконец мать сделала доброе дело и по настоянию своего брата Уильяма Эйскоу и учителя Стокса позволила Исааку вернуться в школу. В 1661 году Ньютон успешно ее окончил и поступил в Тринити-колледж в Кембридже в качестве студента-сайзера. Так тогда называли тех, с кого не брали денег за обучение, но они зарабатывали себе на жизнь, помогая более богатым студентам. Иногда Исаак питался их объедками. (Мать могла себе позволить содержать сына, но этого не делала.) В колледже у него было мало друзей, и такая ситуация сохранится в течение всей его жизни. Он никогда не был женат и, насколько известно, никогда не заводил романов. Он редко смеялся.
Первые два года обучения в колледже были посвящены аристотелевской схоластике, что в то время было стандартом. Но затем разум юноши зашевелился. Прочитав книгу по астрологии, он заинтересовался математикой и обнаружил, что не в состоянии понять ее без знания тригонометрии, а тригонометрию – без знания геометрии, поэтому засел за «Начала» Евклида. Сперва все описанные результаты казались ему очевидными, но все изменилось, когда он добрался до теоремы Пифагора.
В 1664 году Исааку назначили стипендию, и он всерьез погрузился в математику. Изучив стандартные труды того времени, он быстро освоил основы десятичной арифметики, символическую алгебру, пифагоровы тройки, перестановки, кубические уравнения, конические сечения и бесконечно малые. Особенно его увлекли два автора – Декарт с его аналитической геометрией и касательными и Джон Валлис с исследованиями бесконечного и поиском площадей фигур.
Игра со степенными рядами
Изучая зимой 1664–1965 годов трактат Валлиса «Арифметика бесконечного», Ньютон наткнулся на нечто волшебное
[210]. Это был новый способ поиска площадей под кривыми – способ, который был одновременно и простым, и общим.
По сути, он превратил принцип бесконечности в алгоритм. Традиционный принцип бесконечности предлагает вычислять площадь сложной области, представляя ее в виде бесконечного ряда более простых областей. Ньютон следовал этой стратегии, но модернизировал ее, используя в качестве строительных блоков не формы, а символы. Вместо обычных осколков, полосок или многоугольников он использовал степени x, такие как x2 или x3. Сегодня мы называем такую стратегию методом разложения функций в степенные ряды.
Ньютон рассматривал степенные ряды как естественное обобщение бесконечных десятичных дробей. В конце концов, бесконечная десятичная дробь – это не что иное, как бесконечный ряд степеней чисел 10 и 1/10. Цифры в подобного рода записи говорят нам, сколько степеней 10 и 1/10 здесь содержится. Например, числу π = 3,14… соответствует такой ряд:
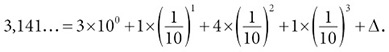
Конечно, чтобы записать любое число этим способом, мы должны разрешить себе использовать бесконечное количество цифр – именно это требует бесконечная дробь. По аналогии Ньютон предположил, что он может составить любую кривую или функцию из бесконечного числа степеней x. Фокус состоял в том, чтобы выяснить, сколько их нужно для искомой комбинации. В ходе своих изысканий он разработал несколько методов поиска нужных сочетаний.
Ньютон наткнулся на свой метод, размышляя о площади круга. Обобщив старую задачу, он обратил внимание на конструкцию, которую раньше никто не замечал. Вместо того чтобы смотреть на стандартные формы вроде целого круга или четверти круга, он занялся фигурой необычной формы – «круговым сегментом» ширины x, где величина x могла быть произвольным числом от 0 до 1, а радиус круга составлял 1.
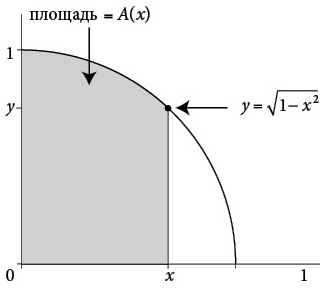
Это был первый творческий шаг. Преимуществом использования величины x было то, что Ньютон мог непрерывно регулировать форму области, словно поворачивая какую-то рукоятку. Небольшое значение x, близкое к 0, давало тонкий вертикальный сегмент круга, тонкую полоску, стоявшую на его краю. Увеличение x утолщало сегмент. Приближение x к 1 давало знакомую форму четверти круга. Меняя x в ту или иную сторону, Ньютон мог получать все промежуточные формы.
С помощью раскованного экспериментирования, распознавания закономерностей и вдохновенных догадок (стиля мышления, почерпнутого из книги Валлиса) Ньютон обнаружил, что площадь круглого сегмента можно выразить с помощью следующего бесконечного степенного ряда: