Именно это и изменилось после Ньютона и Лейбница. Они независимо друг от друга открыли и доказали основную теорему анализа, которая сделала эти задачи стандартными. Теорема связала площади с наклонами, то есть интегралы с производными. Это было потрясающе. Словно в романе Диккенса, два с виду далеких персонажа оказались близкими родственниками. Интегралы и производные были кровной родней.
Влияние этой фундаментальной теоремы было ошеломляющим. Почти в мгновение ока площади стали сговорчивыми. С задачами, которые ранее пытались решить гении, теперь можно было справиться за минуты. Как писал Ньютон одному своему другу, «не существует кривой, выраженной каким-нибудь уравнением… чтобы я не мог меньше чем за четверть часа сказать, можно ли ее квадрировать»
[198]. Понимая, насколько невероятным может прозвучать такое заявление для современников, он продолжал: «Это может показаться смелым утверждением… но мне это очевидно по источнику, откуда я черпаю, хотя я и не берусь доказывать это другим»
[199].
Секретным источником Ньютона была основная теорема анализа. Хотя ни он, ни Лейбниц не были первыми, кто ее сформулировал
[200], они получили все лавры, потому что впервые доказали ее во всей полноте, осознали ее огромную пользу и важность и построили вокруг нее целую алгоритмическую систему. Разработанные ими методы стали обычным делом. Интегралы были обезврежены и превратились в домашние задания для подростков.
Прямо сейчас миллионы школьников и студентов по всему миру решают задачи по математическому анализу, считая один интеграл за другим с помощью основной теоремы. При этом многие даже не замечают подарка, который им преподнесли. И это вполне понятно – ситуация похожа на старый анекдот про рыбу, которая спрашивает свою подругу: «Разве ты не благодарна за воду?» На что вторая рыба отвечает: «А что такое вода?» Учащиеся, имеющие дело с анализом, постоянно погружены в основную теорему и поэтому, естественно, воспринимают ее как должное.
Визуализация основной теоремы с помощью движения
Основную теорему можно понять на интуитивном уровне, размышляя о расстоянии, которое проходит двигающийся объект, например бегун или автомобиль. Познакомившись с таким способом мышления, мы поймем, о чем она говорит, почему верна и почему так важна. Это не просто трюк для нахождения площадей. Это ключ к предсказанию будущего для всего, что нас волнует (в тех случаях, когда это возможно), и к раскрытию секретов движения и изменений во Вселенной.
Основная теорема пришла Ньютону в голову, когда он рассмотрел задачу определения площади с динамической точки зрения. Ему пришла в голову идея внести в эту картину время и движение. Пусть площадь меняется, решил он, и пусть она постоянно увеличивается.
Простейшая иллюстрация его идеи возвращает нас к знакомой задаче с автомобилем, движущимся с постоянной скоростью, для которого пройденное расстояние равно скорости, умноженной на время. Каким бы элементарным ни был этот пример, он все же отражает суть основной теоремы и поэтому подойдет для начала ее рассмотрения.
Представьте, что машина едет по шоссе со скоростью 60 километров в час. Если мы построим график зависимости расстояния от времени и график зависимости скорости от времени, то они будут выглядеть так:
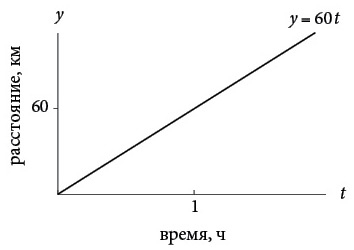
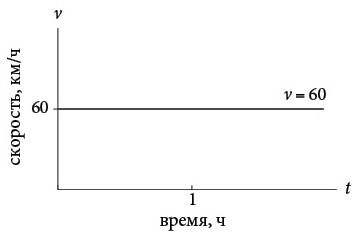
Сначала посмотрим на расстояние в зависимости от времени. Через один час автомобиль проедет 60 километров, через два часа – 120 километров и так далее. В целом расстояние и время связаны соотношением y(t) = 60t, где y(t) – расстояние, пройденное за время t. Я буду называть y(t) = 60t функцией расстояния. Как показано на верхнем рисунке, график функции расстояния – это прямая с наклоном (угловой коэффициент) 60 километров в час. Эта величина сообщает нам скорость автомобиля в любой момент (если бы мы ее еще не знали). В более сложных ситуациях скорость может меняться, но сейчас это простая постоянная функция, v(t) = 60 для любых значений t. Она отображена на нижнем рисунке в виде горизонтальной линии.
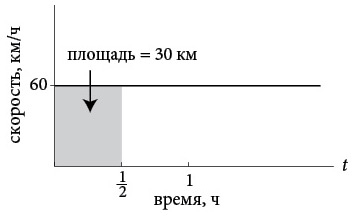
Посмотрев, как скорость проявляет себя на графике расстояния (как наклон прямой), теперь переиначим вопрос и спросим: как расстояние проявляет себя на графике скорости? Иными словами, есть ли на графике скорости какая-нибудь визуальная или геометрическая особенность, которая позволила бы нам увидеть, какое расстояние преодолел автомобиль за любое конкретное время t? Да, есть. Пройденное расстояние – это площадь под кривой скорости (в нашем случае это прямая линия) до момента времени t.
Чтобы понять, почему это так, предположим, что машина проехала какое-то определенное время, например полчаса. В этом случае она проедет 30 километров, поскольку
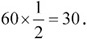 Но суть всего этого в том, что мы можем узнать это расстояние в виде площади серого прямоугольника под прямой между моментами времени t = 0 и
Но суть всего этого в том, что мы можем узнать это расстояние в виде площади серого прямоугольника под прямой между моментами времени t = 0 и
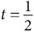 часа.
часа.





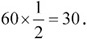 Но суть всего этого в том, что мы можем узнать это расстояние в виде площади серого прямоугольника под прямой между моментами времени t = 0 и
Но суть всего этого в том, что мы можем узнать это расстояние в виде площади серого прямоугольника под прямой между моментами времени t = 0 и
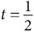 часа.
часа.