Эта формула означает, что каждый день ваш вклад увеличивается на 1/365 часть и это увеличение происходит 365 дней подряд.
Наконец, предположим, что начисление процентов происходит еще чаще. Пусть банк начисляет их раз в год, где n – очень большое число, но при этом ставка пропорционально уменьшается и при каждом начислении составляет 1 / n. Тогда аналогично случаю с 365 начислениями для итоговой суммы получаем формулу
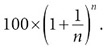
Если устремить n к бесконечности, то итоговая величина вклада будет в 100 раз больше, чем предел величины
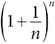 при стремлении n к бесконечности. Этот предел и определяется как число e. Как его вычислить, вовсе не очевидно, но это предельное значение приблизительно равно 2,71828…
при стремлении n к бесконечности. Этот предел и определяется как число e. Как его вычислить, вовсе не очевидно, но это предельное значение приблизительно равно 2,71828…
В банковском деле описанная финансовая конструкция называется непрерывным начислением процентов. Наши результаты показывают, что тут нет ничего чрезвычайного. В описанном примере через год ваш вклад составил бы 100 × e ≈ 271,83 доллара. Это самый лучший возможный результат, но такая сумма всего на 37 центов больше, чем результат начисления раз в день.
Мы перепрыгнули через множество препятствий, чтобы определить e. В итоге e оказалось хитрым пределом. В него встроена бесконечность точно так же, как и в число π для окружностей. Вспомните, что π включает вычисление периметра многоугольников, вписанных в окружность. Такие многоугольники приближаются к окружности по мере того, как количество их сторон n стремится к бесконечности, а длина каждой стороны стремится к нулю. Число e определяется во многом сходным образом, за исключением того, что появляется в другом контексте – при непрерывном начислении процентов.
Показательная функция с основанием e (ее часто называют экспонентой) обозначается ex, подобно тому как показательная функция с основанием 10 записывается как 10x. Поначалу это выглядит странно, но на структурном уровне никаких отличий от основания 10 нет. Все принципы и закономерности те же. Например, если мы хотим найти такое число x, чтобы ex равнялось определенному числу, например 90, мы можем снова использовать логарифмы, как и раньше, но теперь в игру вступает логарифм по основанию e, который называется натуральным логарифмом и обозначается lnx. Чтобы найти такое число x, чтобы ex = 90, включите инженерный калькулятор, введите 90, нажмите кнопку lnx и получите ответ:
Для проверки держите это число на экране и нажмите кнопку ex. Должно получиться 90. Как и раньше, натуральный логарифм и экспонента отменяют действие друг друга, как степлер и антистеплер.
Как бы странно это ни звучало, натуральный логарифм крайне полезен на практике, хотя часто это и незаметно. Прежде всего он лежит в основе эмпирического правила, известного банкирам и инвесторам как «правило 72». Чтобы примерно оценить, через какое время удвоится ваш вклад при данной годовой ставке доходности, нужно разделить 72 на эту ставку. Например, при ставке 6 процентов годовых деньги удвоятся приблизительно через 72 / 6 = 12 лет. Это эмпирическое правило следует из свойств натурального логарифма и экспоненциального роста и хорошо работает при низких процентных ставках
[186].
Кроме того, натуральные логарифмы стоят за радиоуглеродным датированием древних деревьев и костей, а также применяются для определения подлинности произведений искусства. В одном известном случае картины, которые приписывались Вермееру
[187], оказались подделками, что было выявлено с помощью распадающихся изотопов свинца и радия в краске. Как показывают эти примеры, натуральный логарифм сейчас проникает во все области, где есть экспоненциальное увеличение или уменьшение
[188].
Механизм экспоненциального изменения
Повторю самый важный момент, который выделяет e среди других оснований: скорость изменения функции ex – это ex. Следовательно, по мере подъема графика экспоненты ее наклон увеличивается в соответствии с текущей высотой. Чем выше поднимается график, тем круче становится. На языке анализа это утверждение звучит так: ex – это ее собственная производная. Ни одна другая функция не может этим похвастаться
[189]. Это самая удачная из всех функций, по крайней мере, когда дело касается анализа.
Хотя основание e и уникально, остальные показательные функции подчиняются аналогичному принципу возрастания. Разница только в том, что у них рост не строго равен текущему значению функции, а пропорционален ему. Тем не менее этой пропорциональности достаточно, чтобы обеспечить ту взрывную мощь, которую мы связываем с экспоненциальным ростом.
Объяснение для такой пропорциональности должно быть интуитивно понятным. Например, в случае бактерий крупные популяции растут быстрее, потому что чем больше клеток, тем больше возможностей для деления и воспроизведения потомства. То же самое относится и к количеству денег на счете с постоянной ставкой годовых. Чем больше денег, тем больше начисляется процентов, а потому и сумма на счете растет быстрее.
Этот эффект также объясняет вой микрофона, когда он улавливает звук собственного динамика. Динамик содержит усилитель, который делает звук громче. Фактически он умножает уровень громкости на постоянный коэффициент. Если этот более громкий звук улавливается микрофоном, а затем снова отправляется к усилителю, то громкость звука будет многократно увеличиваться в цепи положительной обратной связи. Это вызывает экспоненциальный рост громкости, которая нарастает пропорционально текущему значению, что и приводит к ужасающему визгу.



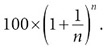
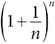 при стремлении n к бесконечности. Этот предел и определяется как число e. Как его вычислить, вовсе не очевидно, но это предельное значение приблизительно равно 2,71828…
при стремлении n к бесконечности. Этот предел и определяется как число e. Как его вычислить, вовсе не очевидно, но это предельное значение приблизительно равно 2,71828…