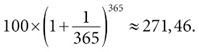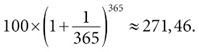и
Обратите внимание на две поразительные вещи:
1. У всех таких логарифмов одинаковая дробная часть: 0,9542…
2. Умножение исходного числа 90 на 10 увеличивает его десятичный логарифм на 1. Умножение на 100 увеличивает логарифм на 2 и так далее.
Мы можем объяснить оба факта, обратившись к правилу: логарифм произведения равен сумме логарифмов Из него следует, что
lg90 = lg(9 × 10) = lg9 + lg10 = 0,9542… + 1
и
lg900 = lg(9 × 100) = lg9 + lg100 = 0,9542… + 2
и так далее. Это объясняет, почему у десятичных логарифмов чисел 90, 900 и 9000 будет одинаковая дробная часть: 0,9542… Она соответствует логарифму числа 9, которое входит множителем в эти числа. Различные степени числа 10 дают целую часть этих чисел (в нашем случае 1, 2 и 3). Вследствие этого нам достаточно работать с десятичными логарифмами чисел от 1 до 10. Они отвечают за дробную часть. Логарифмы всех остальных положительных чисел можно будет выразить через них. У степеней десятки собственная работа: они отвечают за целую часть.
Общее правило для логарифмов в символической форме можно записать следующим образом:
Другими словами, когда мы умножаем два числа и ищем логарифм произведения, результатом будет сумма (а не произведение!) логарифмов отдельных сомножителей. В этом смысле логарифмы заменяют задачу умножения задачей сложения, которая намного проще. Вот почему они, собственно, и были изобретены. Они неизмеримо ускорили вычисления. Вместо того чтобы прикладывать геркулесовые усилия для задач умножения, нахождения квадратных и кубических корней и прочего, математики свели такие вычисления к задачам сложения и эти расчеты стали производиться с помощью готовых таблиц логарифмов. В начале XVII века идея логарифмов уже витала в воздухе, но значительная заслуга в их популяризации принадлежит шотландскому математику Джону Неперу, который в 1614 году опубликовал свое «Описание удивительной таблицы логарифмов». Десять лет спустя Иоганн Кеплер с энтузиазмом использовал новые вычислительные инструменты при составлении астрономических таблиц для положений планет и других небесных тел. Логарифмы были суперкомпьютерами своей эпохи.
Многие люди считают логарифмы сложными, но их смысл можно понять, если провести аналогию с плотницкими работами. Логарифмы и другие функции подобны инструментам. У разных инструментов – разное назначение. Молотки предназначены для забивания гвоздей; дрели – для сверления отверстий; пилы – для разрезания на части. Аналогично показательные функции предназначены для моделирования роста, который подпитывает сам себя, а степенные функции – для моделирования менее агрессивных видов возрастания. Логарифмы полезны по той же причине, что и антистеплер, удаляющий скобки: они отменяют действие другого инструмента. Конкретнее говоря, логарифмы отменяют действие показательных функций, и наоборот.
Рассмотрим показательную функцию 10x и применим ее к какому-нибудь числу, например 3. В результате получим 1000. Чтобы отменить это действие, нажмем кнопку lgx. Применив ее к числу 1000, мы вернемся к исходному числу 3. Функция lgx – логарифм по основанию 10 – отменяет действие функции 10x. В этом смысле указанные функции являются обратными одна другой.
Кроме выполнения роли обратной к показательной функции, логарифмы также описывают многие природные явления. Например, наше восприятие высоты тона примерно логарифмическое. Когда высота тона поднимается на последовательные октавы, от одной ноты до до следующей, такое повышение соответствует последовательным удвоениям частоты соответствующих звуковых волн. Хотя при каждом повышении на октаву волны колеблются вдвое быстрее, мы слышим эти удвоения – которые представляют собой мультипликативные изменения частоты – как равные повышения в тоне, то есть равные аддитивные шаги. Поразительно! Наш мозг дурачит нас, заставляя считать, что 1 так же отстоит от 2, как 2 от 4, 4 от 8 и так далее. Каким-то образом мы ощущаем частоту (впрочем, как и громкость) логарифмически.
Натуральный логарифм и его показательная функция
Каким бы полезным ни было основание 10 в пору своего расцвета, в современном анализе оно редко используется, уступив место другому основанию, которое хоть и выглядит заумно, но оказывается куда более естественным, нежели 10. Оно называется числом e и примерно равно 2,718 (чуть позже я объясню, откуда оно берется), однако его численное значение неважно. Важно то, что показательная функция с этим основанием растет со скоростью, равной самой этой показательной функции.
Позвольте повторить это еще раз.
Скорость роста функции ex в точности равна ex.
Это чудесное свойство упрощает все вычисления с показательными функциями, если они выражены по основанию e. Ни одно другое основание не может похвалиться такой простотой. Работаем ли мы с производными, интегралами, дифференциальными уравнениями или другими инструментами анализа, показательные функции с основанием e всегда самые удобные, самые элегантные и самые красивые.
Помимо роли в упрощении анализа, основание e естественным образом возникает в сфере финансов и банковском деле. Следующий пример показывает, как оно появляется и как определяется.
Представьте, что вы положили в банк 100 долларов при немыслимой, но крайне соблазнительной ставке в 100 процентов годовых. Это означает, что через год ваши 100 долларов превратятся в 200. Теперь начнем сначала и рассмотрим еще более благоприятный сценарий. Допустим, вы убедили банк начислять проценты дважды в год, чтобы вы могли пользоваться процентами с процентов по мере роста вклада. Сколько вы заработаете в этом случае? Учитывая, что вы просите банк начислять проценты вдвое чаще, справедливо, чтобы процентная ставка за полгода составила половину, то есть 50 процентов. Тогда через 6 месяцев вы получите 100 × 1,5 = 150 долларов. А за следующие 6 месяцев, в конце года, сумма вырастет еще на 50 процентов и на вашем счету будет 150 × 1,50 = 225 долларов. Это больше, чем вы получали по первоначальной договоренности, поскольку теперь вам начисляют проценты на проценты.
Теперь ответим на вопрос, что произойдет, если вы сможете убедить банк начислять проценты еще чаще, пропорционально уменьшая процентную ставку для каждого периода начисления? Станете ли вы баснословно богаты? К сожалению, нет. Если начислять проценты раз в квартал (то есть четыре раза в год), то в конце года на счету будет 100 × 1,254 ≈ 244,14 доллара – не намного больше по сравнению с 225. Если начислять проценты каждый день, то есть 365 раз в год, то вы получите в конце года всего лишь