Эти четыре параметра – a, b, c, T – можно представлять как четыре рукоятки, которые позволяют регулировать форму и положение синусоиды. Они действуют так: b-рукоятка перемещает синусоиду вверх и вниз; c-рукоятка двигает ее влево и вправо; T-рукоятка контролирует, как быстро волна колеблется, сжимая и растягивая ее по горизонтальной оси; и, наконец, a-рукоятка определяет, насколько сильный размах у колебаний.
Если бы мы могли каким-то образом настроить эти рукоятки так, чтобы синусоида проходила через все нарисованные нами ранее точки, то это позволило бы существенно сжать информацию и означало бы, что вместо 27 значений мы бы обошлись всего четырьмя параметрами такой подобранной синусоиды, то есть сжали бы данные в 27/4 = 6,75 раза. В реальности же, поскольку у нас один из параметров – год, по сути, мы можем играть всего с тремя параметрами, что дает нам сжатие в 27/3 = 9 раз. Такое уменьшение возможно, потому что наши данные не случайны. Они подчинены некоторой закономерности, а синусоида воплощает ее и делает за нас всю работу.
Единственная загвоздка – отсутствие синусоиды, которая бы идеально проходила через все точки. Этого следует ожидать при подгонке к реальным данным идеализированной модели: определенные расхождения неизбежны, но всегда есть надежда, что они окажутся незначительными. Для их минимизации требуется найти синусоиду, которая максимально близко подходит к нашим точкам. Вот тут-то в игру и вступает анализ.
На рисунке ниже показана наилучшая синусоида, определяемая алгоритмом оптимизации, который я объясню чуть ниже.
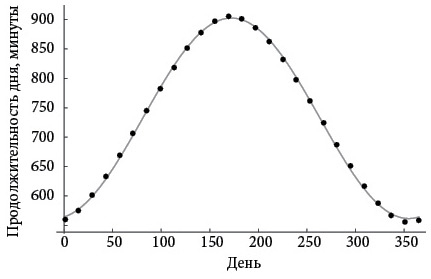
Но сначала обратите внимание, что результирующая кривая подходит не идеально. Например, она недостаточно низка в декабре, когда дни очень короткие и данные попадают ниже кривой. Тем не менее простая синусоида, безусловно, отражает суть происходящего. В зависимости от наших целей такое качество приближения может оказаться достаточным.
Но при чем тут анализ? Он помогает оптимально выбрать четыре параметра. Представьте, что вы поворачиваете эти четыре рукоятки, добиваясь наилучшей настройки, – нечто вроде поворота ручек на радиоприемнике для получения самого сильного сигнала. Фактически это то, что делал Ферма в задаче с багажной полкой, когда искал параметры самой вместительной коробки. Он менял единственный параметр x, длину боковой стороны коробки, и искал сигнал о максимальном объеме коробки. В нашем же случае требуется настроить четыре параметра. Однако основная идея та же. Мы должны добиться сигнала оптимальности, меняя четыре параметра.
Если подробнее, то работает это так. Мы вычисляем погрешность (иными словами, ошибку) для любого конкретного набора значений для четырех параметров, то есть разницу между соответствующей синусоидой и реальными данными во всех 27 точках года. Естественный критерий при выборе наилучшей кривой – чтобы общая ошибка по всем 27 точкам была настолько мала, насколько это возможно. Однако при этом общая ошибка – не самая удачная вещь, потому что нам не нужно, чтобы отрицательные ошибки компенсировали положительные и в результате складывалось ложное впечатление, что кривая подходит хорошо, хотя в реальности это не так. Отклонения вниз так же плохи, как и вверх, и от обоих нужно избавляться; нельзя допускать, чтобы они компенсировали друг друга. По этой причине математики рассматривают не ошибки, а квадраты ошибок. Такая мера отклонения будет всегда неотрицательной, и отклонения в разных точках не смогут при сложении аннулировать друг друга. (Это один из примеров практической пользы правила, что отрицательное число, умноженное на отрицательное, будет положительным. Квадрат отрицательной ошибки дает положительную меру погрешности, как нам и нужно.) Итак, основная идея при подборе четырех параметров синусоиды – минимизировать общую квадратичную ошибку для кривой. Этот подход называется методом наименьших квадратов и работает лучше всего, когда данные подчинены какой-то закономерности, как в нашем случае.
Все это приводит к крайне важному общему выводу: именно закономерности в первую очередь и обеспечивают сжатие. Сжать можно только данные, следующие какому-то шаблону. Со случайными данными это не получится. К счастью, многие вещи, которые интересны людям – отпечатки пальцев, песни и лица, – хорошо структурированы и обладают закономерностями. Подобно тому как продолжительность дня следует простой синусоиде, фотография лица включает брови, дефекты кожи, скулы и прочие характерные признаки. В песнях есть мелодия, гармония, ритмы и динамика. В отпечатках имеются гребни, петли и завитки. Будучи людьми, мы мгновенно распознаем эти закономерности. Компьютеры тоже можно научить их распознавать. Синусоиды идеально подходят для отображения периодических закономерностей, но менее пригодны для представления более резко локализованных особенностей, таких как края ноздрей или родинок.
Для этой цели исследователи, работающие в различных областях, придумали кривые, которые называются вейвлетами
[171]. Эти маленькие волны более локализованы, чем синусоиды. Они не распространяются в обоих направлениях, а сильно сконцентрированы во времени и пространстве.
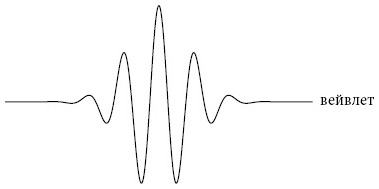
Вейвлеты внезапно появляются, несколько раз колеблются, а затем исчезают. Они похожи на сигналы кардиомониторов или всплески активности, регистрируемые сейсмографами при землетрясениях. Они идеально подходят для изображения резкого всплеска при регистрации мозговых волн, толстого мазка на картине Ван Гога или морщины на лице.
ФБР использовало вейвлеты
[172] для преобразования файлов с отпечатками пальцев. Со времени внедрения практики применения отпечатков в начале XX века они хранились в виде чернильных оттисков на бумажных носителях. К середине 1990-х фонды разрослись примерно до двух миллионов карточек и занимали почти половину гектара офисных площадей. Когда ФБР решило оцифровать эти досье, специалисты превратили их в полутоновые изображения с 256 уровнями серого цвета и разрешением в 500 точек на дюйм, вполне достаточным для улавливания всех мелких завитков, петель, краев гребней, разветвлений и прочих идентифицирующих деталей.




