Оптимизация багажной полки
Зачаточная версия дифференциального исчисления Ферма выросла из применения его алгебраических методов к задачам оптимизации
[166]. Оптимизация – это изучение способов сделать что-то наилучшим образом. В зависимости от контекста наилучший может означать быстрейший, наибольший, самый дешевый, самый выгодный, наиболее эффективный или какое-то иное понятие оптимальности. Чтобы проиллюстрировать свои идеи самым простым способом, Ферма придумал несколько задач, очень похожих на те упражнения, которые мы, преподаватели математики, до сих пор задаем нашим ученикам. Так что они могут винить напрямую его.
Одна из этих задач, приспособленная к современным реалиям, выглядит примерно так. Представьте, что вы хотите сделать коробку, в которой помещается как можно больше вещей, при соблюдении двух ограничений. Во-первых, коробка должна быть квадратной в сечении, то есть ее ширина и длина должны быть по x сантиметров. Во-вторых, она должна помещаться на верхней багажной полке определенной авиакомпании. Согласно ее правилам перевозки багажа, сумма трех измерений любого предмета багажа (в нашем случае – сумма ширины, длины и высоты коробки) не должна превышать 45 дюймов. Какой выбор параметра x даст коробку наибольшего объема?
Один из способов решить задачу – использовать здравый смысл. Попробуйте несколько вариантов. Скажем, пусть длина и ширина коробки будут по 10 дюймов. Тогда на высоту останется 25 дюймов, потому что 10 + 10 + 25 = 45. Объем коробки с такими размерами составит 10 × 10 × 25 = 2500 кубических дюймов. Но, может быть, коробка кубической формы будет лучше? Поскольку у куба длина, ширина и высота одинаковы, то коробка должна иметь размеры 15 × 15 × 15 дюймов, что даст объем 3375 кубических дюймов. Если вы повозитесь еще с некоторыми другими размерами, то придете к выводу, что именно куб – оптимальный выбор для формы коробки. И это действительно так.
Эта задача сама по себе не сложная, но она позволяет показать, как именно Ферма рассуждал в ходе ее решения, так как его подход привел к значительно более серьезным вещам.
Как и в большинстве алгебраических задач, первым делом следует перевести всю имеющуюся информацию в символы. Поскольку длина и ширина коробки равны x, то их сумма составит 2x. А учитывая, что высота плюс ширина плюс длина не могут превышать 45 дюймов
[167], на высоту остается 45 – 2x дюймов. Таким образом, объем коробки равен x × x × (45 – 2x) кубических дюймов. В результате умножения получаем 45x2 – 2x3. Это и есть объем коробки. Обозначим его V(x). Итак,
Если мы сейчас на мгновение сжульничаем и с помощью компьютера построим график, отложив x по горизонтали, а V по вертикали, то увидим, как кривая возрастает и достигает максимума при x = 15 дюймов, как и ожидалось, а потом снова спускается к нулю.
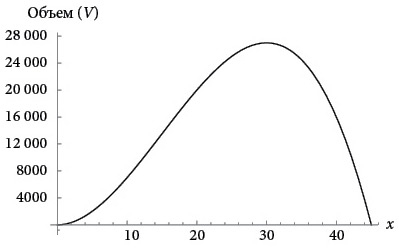
Широко используемый сегодня альтернативный способ найти это максимальное значение с помощью дифференциального исчисления – вычислить производную функции V(x) и приравнять ее к нулю. В верхней точке кривой угол наклона равен нулю: кривая тут не поднимается и не опускается. Поэтому, если определять наклон через производную (как мы увидим в главе 6), то в точке максимума она должна быть равна 0. Немного алгебры и применения различных правил для производных – и мы получим для точки максимума то же самое значение x = 30.
Однако у Ферма не было компьютеров и графопостроителей, и, конечно же, он не оперировал понятием производной; наоборот, выдвинутые им идеи и привели к производным! Так как же он решал эту задачу? Он использовал особое свойство максимума: горизонтальная линия ниже максимума пересекает кривую в двух точках, как показано ниже, в то время как горизонтальные линии выше максимума вообще не пересекают кривую.
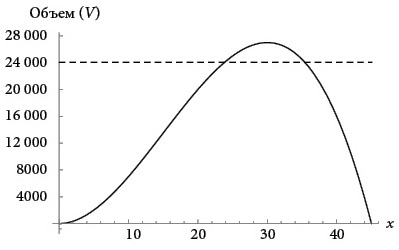
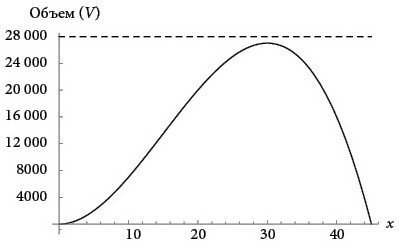
Это подсказывало интуитивную стратегию решения задачи. Представьте, что вы медленно поднимаете горизонтальную линию, начиная ниже максимума. По мере ее постепенного перемещения вверх две точки пересечения с кривой двигаются по ней навстречу друг другу, словно бусины в ожерелье.
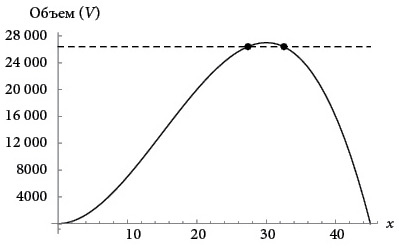
В максимуме эти две точки сливаются. Наблюдение за их слиянием и позволило Ферма определить максимум. Он вывел условие, при котором две точки сливаются в одну, образуя так называемое двойное пересечение. С такой идеей все остальное – чистая алгебра, простое манипулирование символами. Это выглядит так.
Предположим, что наши два пересечения происходят в точках x = a и x = b. Тогда, поскольку по построению точки пересечения находятся на одной горизонтальной линии, должно быть справедливо V(a) = V(b). Следовательно,
Теперь полезно перегруппировать слагаемые. Перенесем квадраты в одну часть, а кубы в другую и получим
Вспомнив школьную алгебру, разложим обе части на множители и получим
45(a – b)(a + b) = 2(a – b)(a2 + ab + b2).
Разделим обе части на общий множитель a – b. Это корректное действие, поскольку предполагается, что a и b различны (если бы они были одинаковыми, то деление на a – b означало бы деление на 0, что запрещено, как мы говорили в главе 1). В результате получим уравнение






