Он повторял эксперимент много раз, иногда меняя наклон ската, а иногда – расстояние, проходимое шаром. По его словам, он установил следующее: «Расстояния, пройденные за равные промежутки времени телом, падающим из состояния покоя, находятся между собой в таком же соотношении, как и нечетные числа, начинающиеся с единицы»
[114].
Чтобы понятнее изложить этот закон больших чисел, предположим, что шар прокатится некоторое расстояние за первую единицу времени. Тогда за вторую единицу времени он прокатится втрое дальше, за третью – впятеро.. Это потрясающе! Нечетные числа 1, 3, 5 и так далее как-то связаны с тем, как предметы катятся вниз. И если падение – это предельный случай качения, когда наклон приближается к вертикали, то и для падения должно быть справедливо то же самое.
Мы можем только представить, как должен был обрадоваться Галилей, когда открыл это правило. Но обратите внимание, как он его сформулировал: словами, числами и соотношениями, а не буквами, формулами и уравнениями. Наша нынешняя манера использовать алгебру, а не разговорный язык, по тем временам казалась бы авангардным, новейшим, новомодным способом думать и говорить. Галилей так не думал и не выражался, да и читатели его бы не поняли.
Чтобы увидеть самые важные следствия из правила Галилея, давайте посмотрим, что произойдет при сложении последовательных нечетных чисел. За одну единицу времени шар прошел одну единицу расстояния. За следующую – еще три единицы расстояния, то есть в общей сложности 1 + 3 = 4 единицы с момента начала движения. После третьей единицы времени получаем 1 + 3 + 5 = 9 единиц расстояния. Обратите внимание на закономерность: числа 1, 4 и 9 – это квадраты последовательных целых чисел: 12 = 1, 22 = 4, 32 = 9. Таким образом, правило нечетных чисел Галилея, похоже, означает, что общее расстояние, пройденное падающим телом, пропорционально квадрату прошедшего времени.
Эту изящную связь между нечетными числами и квадратами можно доказать наглядно. Представьте нечетные числа как «уголки» из точек:
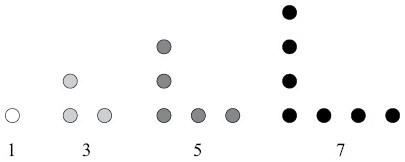
Теперь соедините их так, чтобы получился квадрат. Например, 1 + 3 + 5 + 7 = 16 = 4 × 4, поскольку мы можем сложить первые четыре уголка так, чтобы они образовали квадрат со стороной 4.

Наряду с законом о расстоянии, пройденном падающим телом, Галилей также открыл закон скорости. По его словам, скорость увеличивается пропорционально времени падения. Интересно здесь то, что ученый имел в виду мгновенную скорость, что кажется парадоксальным понятием. В книге «Две новые науки» он приложил немало усилий, чтобы объяснить, что при падении из состояния покоя тело не прыгает внезапно с нулевой скорости до какой-то более высокой, как полагали его современники. Наоборот, оно плавно проходит через все промежуточные скорости – бесконечное количество скоростей – за конечное время, начиная с нулевой и непрерывно увеличивая скорость при падении.
Итак, в этом законе падающих тел Галилей инстинктивно размышлял о мгновенной скорости – понятии дифференциального исчисления, с которым мы познакомимся в главе 6. В то время он не мог определить ее точно, но интуитивно понимал.
Искусство научного минимализма
Прежде чем мы оставим эксперимент Галилея с наклонной плоскостью, давайте обратим внимание на стоящее за ним мастерство. Ученый уговорил природу дать красивый ответ, задав красивый вопрос. Словно художник-экспрессионист, он выделял то, что его интересовало, отбрасывая остальное.
Например, описывая свой прибор, он говорит, что сделал желоб очень прямым, гладким и отполированным
[115] и катил по нему твердый, гладкий и круглый бронзовый шар. Почему его так беспокоили гладкость, прямолинейность, твердость и округлость? Потому что ученый хотел, чтобы шар катился вниз в самых простых и идеальных условиях, какие он только мог представить. Он сделал все возможное, чтобы уменьшить потенциальные осложнения, возникающие из-за трения или столкновений шара с боковыми стенками желоба (что могло происходить, если канал не был прямым), из-за мягкости шара (что могло привести к потере энергии шаром из-за его деформации) и всего остального, что могло вызвать отклонения от идеального случая. Это был правильный эстетический выбор. Просто. Элегантно. И минимально.
Сравните это с Аристотелем, который ошибался с законами падения, потому что его сбивали с толку осложнения. Ученый считал, что тяжелые тела падают быстрее легких – со скоростью, пропорциональной их массе. Это верно для крошечных частиц, плавающих в очень густой вязкой среде, например патоке или меде, но неверно для пушечных ядер или мушкетных пуль, падающих сквозь воздух. Похоже, Аристотель был так озабочен силами сопротивления, создаваемыми воздухом (следует признать, что это важный эффект при падении перьев, листьев, снежинок и прочих легких предметов, у которых большая площадь поверхности, на которую воздействует воздух), что забыл проверить свою теорию на более типичных предметах вроде камней, кирпичей или обуви, то есть на компактных и тяжелых вещах. Другими словами, он слишком сильно сосредоточился на шуме (сопротивлении воздуха) и недостаточно на сигнале (инерция и сила тяжести)
[116].
Галилей не позволил себе отвлекаться. Он знал, что сопротивление воздуха и трение в реальном мире неизбежны, а значит, и в его эксперименте тоже, но они несущественны. Предвидя критику, он признал, что дробинка падает не так быстро, как пушечное ядро, но отметил, что допущенная ошибка гораздо меньше, чем в теории Аристотеля. В книге «Две новые науки» персонаж, прототипом которого был Галилей, говорит простоватому собеседнику, стоящему на аристотелевских позициях
[117]: «Я не хотел бы… чтобы вы поступали как многие другие, отклоняя беседу от главного вопроса, и придирались к выражению, в котором я допустил отклонение от действительности на один волосок, желая скрыть за этой небольшой погрешностью ошибку другого, грубую, как якорный канат»
[118],
[119].




