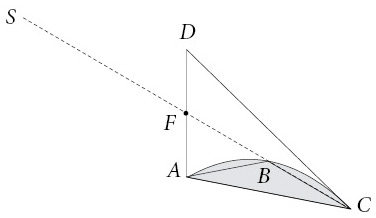
И вот тут появляется ошеломляющая идея, лежащая в основе всей концепции. Используя известные факты о параболах и треугольниках, Архимед доказывает, что можно уравновесить большой внешний треугольник относительно сегмента параболы, если представлять его по одной вертикальной линии за раз. Он считает обе фигуры состоящими из бесконечного количества параллельных отрезков, похожих на бесконечно тонкие планки или ребра. Вот типичная пара вертикальных линий-ребер. Короткое ребро соединяет основание с параболой,
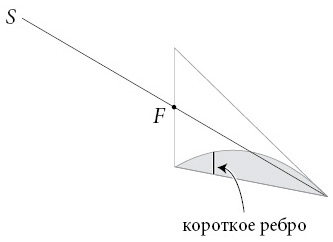
а длинное ребро – с верхней стороной внешнего треугольника.
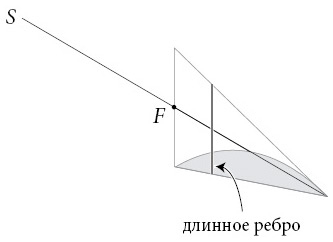
Суть идеи состоит в том, что эти ребра идеально уравновешивают друг друга, как дети, качающиеся на доске, если они находятся в правильных точках. Архимед доказывает, что если сдвинуть короткое ребро до точки S, а длинное оставить на своем месте, то они уравновешиваются.
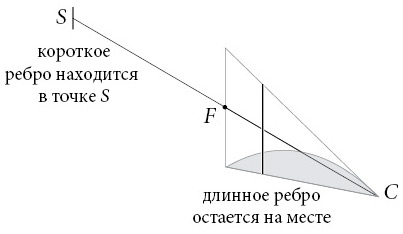
То же самое верно для любого вертикального кусочка. Неважно, какой вертикальный срез вы сделаете, короткое ребро всегда уравновесит длинное, если вы поместите его в точку S, а длинное оставите на месте.
Поэтому две фигуры уравновешивают друг друга: ребро за ребром. Если перенести все ребра параболы в S, то они уравновешивают все ребра внешнего треугольника ACD. Соответственно, вся масса параболы, перемещенная в S, уравновешивает внешний треугольник, находящийся там, где он есть.
Далее Архимед заменяет весь внешний треугольник одной эквивалентной точкой под названием центр тяжести треугольника. Эта точка – словно «заместитель» треугольника. Весь треугольник воздействует на доску качелей так, будто вся его масса сосредоточена в одной точке – центре тяжести. Этот центр, как Архимед уже показал в другой работе, лежит внутри треугольника на линии FC в точке, расстояние от которой до F ровно в три раза меньше, чем расстояние SF.
Итак, у нас получается рычаг, где вся масса параболы в точке S уравновешивает массу треугольника (сосредоточенную в одной точке), причем длинное плечо рычага втрое длиннее короткого. Следовательно, по закону рычага масса параболы втрое меньше площади треугольника. Это означает, что площадь сегмента параболы составляет треть от площади треугольника ACD. Однако ранее мы уже взяли на заметку тот факт, что ACD вчетверо больше ABC. Поэтому площадь сегмента параболы составляет 4/3 от площади треугольника ABC внутри него… Тот же результат, что мы получили, находя площадь с помощью бесконечного ряда из треугольных осколков!
Надеюсь, мне удалось передать всю психоделичность этого рассуждения. Здесь Архимед уже больше похож не на гончара, собирающего черепки, а на мясника. Он делит ткань параболической области, по одной вертикальной полоске за раз, и подвешивает эти бесконечно тонкие полоски на крюке в точке S. Общий вес мяса остается таким же, как если бы это был исходный цельный сегмент параболы. Просто он порезал исходную фигуру на множество вертикальных тончайших полосок, висящих на одном крюке. (Хм, странный образ. Возможно, нам лучше придерживаться терминологии доски-качалки?!)
Почему я назвал это рассуждение трансгрессивным? Потому что оно оперирует актуальной бесконечностью. На каком-то этапе Архимед открыто описывает внешний треугольник как «составленный из всех параллельных линий»
[65]. Конечно, в греческой математике это было табу – вся эта бесконечная совокупность вертикальных линий, все эти вертикальные ребра. Он открыто представляет треугольник как уже завершенную бесконечность – совокупность ребер. И, делая это, выпускает голема на свободу.
Точно так же он описывает сегмент параболы – как «состоящий из всех параллельных линий, нарисованных внутри фигуры»
[66]. Привлечение актуальной бесконечности, по его оценке, понижает статус этого рассуждения до эвристического – то есть это средство найти ответ, но не доказать его правильность. В письме Эратосфену он преуменьшает значение метода, говоря, что это не более чем своего рода указание на то, что вывод будет верным
[67].
Каким бы ни был статус метода Архимеда, он обладает свойством e pluribus unum. Это латинское выражение, означающее «из многих – единое», используется как девиз на гербе США. Из бесконечного множества отрезков, составляющих параболу, возникает единая область. Думая о ней как о массе, Архимед перемещает ее, отрезок за отрезком, на левое сиденье доски-качалки. Теперь бесконечность отрезков представлена массой, сосредоточенной в одной точке. Единое заменяет многое, представляя его точно и верно.
То же самое справедливо и для уравновешивающего внешнего треугольника на правой стороне доски. Континуум вертикальных линий превращается в одну точку – центр тяжести. Она тоже заменяет целое. Бесконечность схлопывается в единое, e pluribus unum. Только это не поэзия и не политика, а истоки интегрального исчисления. Треугольники и сегменты парабол каким-то таинственным образом в каком-то смысле, который Архимед не смог строго определить, явно эквивалентны бесконечности из вертикальных линий.
Хотя Архимеда, похоже, смущает его заигрывание с бесконечностью, у него хватает смелости в этом признаться. Любой, кто пытается измерить криволинейную форму – найти длину границы или объем, который она заключает, – вынужден сражаться с пределом бесконечных сумм бесконечно малых частей. Осторожные люди могут попытаться обойти эту необходимость с помощью метода исчерпывания. Но на деле от нее никуда не деться. Справляться с криволинейными формами – так или иначе значит справляться с бесконечностью. Архимед открыто об этом говорит. Когда ему нужно, он может нарядить свои доказательства в респектабельные одежды, используя конечные суммы и метод исчерпывания. Но в глубине души он лукавит. Он признает, что мысленно взвешивает фигуры, мечтает о рычагах и центрах тяжести, взвешивая области и твердые тела отрезок за отрезком, по одному бесконечно малому кусочку за раз.






