Мы никогда не узнаем всех цифр числа π. Тем не менее они ожидают своего открытия. На момент написания этой книги лучшие компьютеры мира вычислили 22 триллиона цифр. И все же 22 триллиона – ничто по сравнению с бесконечным количеством цифр, определяющих π. Подумайте, насколько это тревожно с философской точки зрения. Я сказал, что цифры числа π есть, но где именно? В материальном мире их нет. Они существуют в какой-то платоновской реальности вместе с абстрактными понятиями вроде истины и справедливости.
В числе π есть нечто парадоксальное. С одной стороны, оно представляет собой порядок, воплощенный в форме круга, который долгое время считался символом совершенства и вечности. С другой же стороны, π – непокорное, внешне неопрятное число, его цифры не подчиняются никаким явным правилам, по крайней мере тем, которые мы можем воспринимать
[56]. Число π неуловимо и загадочно, навеки недостижимо. Столь завораживающим его делает сочетание в нем порядка и беспорядка.
По большому счету π – это дитя анализа. Оно определяется как недостижимый предел нескончаемого процесса. Но, в отличие от последовательности многоугольников, неуклонно приближающихся к окружности, или незадачливого пешехода, проходящего половины половин пути к стене, у π нет предела, который мы можем узнать. И тем не менее π существует. Вот оно, четко определенное как отношение двух длин, лежащих перед нами: длины окружности и ее диаметра. Это отношение определяет π, причем максимально ясно, хотя само число ускользает сквозь наши пальцы.
Со своими началами инь и ян число π напоминает весь анализ в миниатюре. Это портал между круглым и прямолинейным, бесконечно сложное число, баланс между порядком и хаосом. В свою очередь, анализ использует бесконечное для изучения конечного, неограниченное для изучения ограниченного, прямое для изучения кривого. Принцип бесконечности – ключ к разгадке тайны кривых, и впервые он возник здесь, в загадке π.
Кубизм встречается с анализом
Архимед углубился в загадку кривых, снова руководствуясь принципом бесконечности, в своем труде под названием «Квадратура параболы»
[57]. Парабола – это кривая, которую описывает мяч при броске или струйка воды из фонтана. На самом деле эти дуги в реальном мире можно считать параболами только приближенно. Согласно Архимеду, настоящая парабола получается при сечении конуса плоскостью
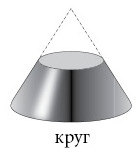
[58]. Представьте себе нож, который разрезает колпак или конический бумажный стаканчик; при разрезе могут получиться разные виды кривых – в зависимости от того, под каким углом нож будет резать конус. Разрез параллельно основанию конуса образует окружность.
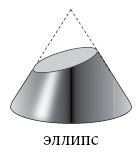
Если провести разрез немного наклонно, получится эллипс.
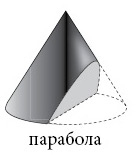
Если угол разреза будет таким же, как у самого конуса, получится парабола.
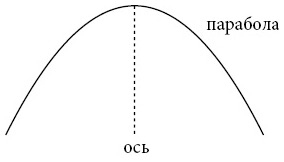
Если посмотреть на плоскость разреза, то парабола выглядит как изящная симметричная кривая. Линия симметрии называется осью параболы.
В своем труде Архимед поставил перед собой задачу вычислить площадь сегмента параболы. Говоря современным языком, сегментом параболы называется криволинейная область, лежащая между параболой и пересекающей ее прямой.
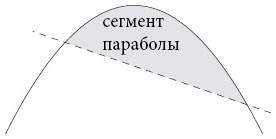
Термином «квадратура» называется определение площади какой-либо фигуры (изначально – построение квадрата, равновеликого этой фигуре), то есть поиск способа выразить ее через более простые формы – квадрат, треугольник, прямоугольник и прочие прямолинейные фигуры.
Архимед использовал потрясающую стратегию. Он представил сегмент параболы как бесконечное множество треугольных черепков, склеенных вместе, словно осколки разбитого глиняного горшка.
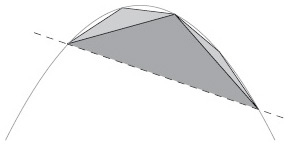
Эти осколки образуют бесконечную иерархию размеров: один большой треугольник, два поменьше, четыре еще меньше и так далее. Ученый планировал найти их площади, а затем сложить их и вычислить интересующую его площадь. Требовался калейдоскопический скачок художественного воображения, чтобы представить плавный сегмент в виде мозаики из угловатых кусков. Если бы Архимед был художником, он стал бы первым кубистом.








