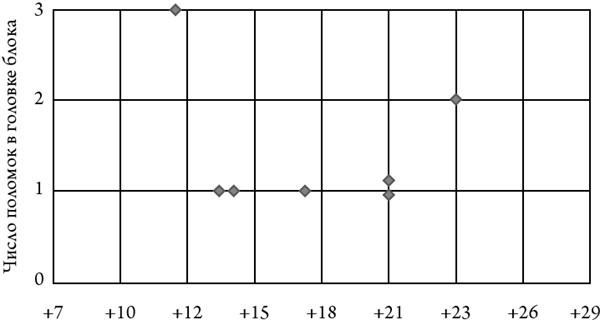
Дмитрий настроен против участия в гонке. Он согласен с тем, что между поломками головки блока и изменениями температуры не существует прямой взаимосвязи; в трех случаях поломка произошла в самый прохладный день гонки (+11 ⁰С), а в двух других – в самый жаркий (+24 ⁰С). Но что если существует некий оптимальный диапазон – не слишком жарко, но и не слишком холодно? «Если поломки случайны, то вероятность того, что вы выйдете из гонки, и того, что войдете в пятерку лучших, одинаково равна 50 %, – говорит Дмитрий. – Но если они происходят не случайно, то степень вероятности ниже. В этот день температура на небывало низком уровне. Мы не знаем, есть ли взаимосвязь между поломками двигателя и изменениями температуры, но если она есть, то двигатель точно сломается». Джулия считает, что слова механика Пэт о температуре – «полная ерунда», но, как и Дмитрий, считает проблему двигателя «черным ящиком», не дающим команде информации, которая позволяет расчитать вероятность победы или поражения в сегодняшней гонке. Она также признает собственное стремление избежать риска и не приняла бы участия в гонке.
Все участники команды, кроме Дмитрия, соглашаются с тем, что «нет никакой корреляции» между температурой и поломкой двигателя. «Я что, остался один?» – спрашивает Дмитрий, и несколько человек хихикают.
Джейк меньше всех проникся доводами механика Пэта. «Я думаю, Пэт очень хороший механик, – говорит он, – но, на мой взгляд, анализ коренных причин у него выходит неважно – это ведь совсем другая область». Джейк считает, что Пэт пал жертвой известного когнитивного стереотипа – переоценки важности впечатляющего воспоминания: о том, что три поломки головки блока произошли в прохладный день. «Мы не обладаем информацией, необходимой для понимания этого графика, – говорит Джейк. – Всего было двадцать четыре гонки, так? Сколько из них проходило при температуре +11 °C без поломки двигателя? Я вовсе не хочу нападать на тебя», – говорит он Дмитрию, улыбаясь и хлопая его по руке.
Все соглашаются с тем, что было бы не лишним иметь сведения о температуре, но работать приходится с тем, что есть. Джастин выражает мнение всех сторонников участия в гонке: «Я просто думаю, что надо принять участие – иначе зачем вообще было идти в этот бизнес?»
Похоже, группа вновь вернулась в исходное положение, снова идет голосование против гонки – до тех пор, пока Мей не пересматривает свои расчеты. «Я передумала, – говорит она. – Я голосую за гонку». Сравнив потенциальные финансовые риски и прибыли, Мей пришла к выводу, что команде Картера нужна всего лишь 26 %-ная вероятность попадания в пятерку лучших (то есть половина текущего рейтинга) для того, чтобы гонка завершилась в их пользу. И даже если прохладная погода повлияет на эту вероятность, «она не будет ниже 26 %, так что нам ничего не грозит». Она считает, что Дмитрий трактует полученные сведения предвзято; команда Картеров участвовала в гонке при температуре от +11 до +27 °C, при этом несколько случаев поломки имели место при температуре ниже +18 °C, а три – при более высокой температуре. По ее мнению, Дмитрий чересчур зацикливается на температуре +11 °C, потому что именно при ней произошли три поломки головки. Но ведь мотор сломался всего один раз.
Джейк вмешивается в разговор и говорит, что раз каждый участник группы трактует график по-своему, «может быть, имеет смысл вынести вопрос на всеобщее обсуждение». Ему нравится довод Мей об ожидаемой прибыли и убытках. «На мой взгляд, это единственное конкретное решение – всегда хорошо основываться на математике… Если бы мне сказали, что, подбросив монетку и проиграв, я потеряю 100 долларов, но если выиграю, то получу 200, я бы только и делал, что подбрасывал бы ее». Он напоминает группе, что в последних двух гонках команда Картера проводила процедуру подготовки двигателя, и никаких проблем не возникало. «Этих сведений недостаточно, – говорит он, – но, по крайней мере, они не противоречат моим доводам».
«При какой температуре тебе было бы комфортнее участвовать в гонке?» – спрашивает Мей Дмитрия. «У нас было две поломки двигателя при температуре +21 °C, одна при +17 °C и одна при +11 °C. Для нас не существует безопасной температуры». Дмитрий хочет установить температурный диапазон в рамках, с которыми они уже имели дело. Что-то работает не так, как должно, поэтому любые отклонения от температурного диапазона могут привести к неизвестным последствиям. Он знает, что его рекомендация – исключительно субъективна.
Группа подходит к финишной прямой. После перехода Мей соотношение сил – четыре к трем, а это значит, что гонке быть. Студенты продолжают дискуссию, запихивая в рюкзаки и папки бумаги по ситуативной задаче.
Мартина быстро зачитывает часть задачи, в которой хозяин команды Би Джей Картер спросил мнение своего главного механика Робина. «Участники гонок постоянно рискуют жизнью. Я лично всякий раз рискую карьерой, а вы – деньгами, которые вкладываете в этот бизнес», – сказал ему Робин. Никто еще не выиграл гонку, сидя на трибуне, напомнил он своему боссу.
Мартина задает последний вопрос: «Получается, все дело в деньгах, так? Никто ведь не умрет, если мы примем участие в гонке?»
Несколько участников группы переглядываются и смеются, а потом все расходятся. Придя в класс на следующий день, студенты узнают, что большинство тех, кто когда-либо получал задание о гонке Картеров, приняли решение участвовать в гонке. Преподаватель обходит класс, прося студентов привести логическое обоснование своих доводов в пользу или против участия.
Те команды, которые решили участвовать, обсуждают оценку вероятности и алгоритмы решений. Студенты разделяются во мнениях о том, представляет ли поломка двигателя в середине гонки угрозу для жизни водителя. Большинство считает, что сведения о температуре – это отвлекающий маневр. Одна женщина говорит: «Если мы хотим чего-то добиться в гоночном бизнесе, нужно уметь принимать подобные риски». Многие согласно кивают. Ее команда единодушно проголосовала за гонку (7–0).
Дмитрий возражает, и преподаватель устраивает ему безжалостный допрос. По мнению Дмитрия, ни один из алгоритмов решений, которые составили группы, не имеет значения, если отказаться от предположения, что поломка двигателя происходит случайно. Он прибавляет, что данные эти особенно неоднозначны, потому что по какой-то причине главный механик не включил в график те показатели температуры, при которых двигатель не ломался.
– Ладно, Дмитрий, тогда у меня количественный вопрос, – говорит профессор. – Сколько раз вчера я повторил: «Если вам нужна дополнительная информация, спрашивайте»?
По классу прокатываются приглушенные «ахи» и «охи».
– Четыре, – сам себе отвечает профессор. – Четыре раза я сказал: «Если вам нужна дополнительная информация, спрашивайте».
Ни один студент не обратился, чтобы получить недостающие данные. Профессор чертит новый график, отображая на нем все гонки. График получается такой:



