Независимые (совместные) события
Если вы одновременно бросаете монету и кубик, то шанс получить «орел» и 6 равняются
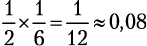 , или 8 %. Когда исход одного события не влияет на исход другого, их называют независимыми. Вероятность получить сочетание конкретных результатов двух независимых событий равна произведению вероятностей каждого из них.
, или 8 %. Когда исход одного события не влияет на исход другого, их называют независимыми. Вероятность получить сочетание конкретных результатов двух независимых событий равна произведению вероятностей каждого из них.
Резервное хранение
 Вам нужно организовать хранение данных в течение года. Один диск имеет вероятность сбоя 1 на 1 млрд. Другой стоит 20 % от цены первого, но в его случае вероятность сбоя — 1 на 2000. Какой диск вам следует купить?
Вам нужно организовать хранение данных в течение года. Один диск имеет вероятность сбоя 1 на 1 млрд. Другой стоит 20 % от цены первого, но в его случае вероятность сбоя — 1 на 2000. Какой диск вам следует купить?
Если вы решите использовать три дешевых диска, то потеряете данные, только если все три выйдут из строя. Вероятность того, что это произойдет, равняется
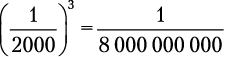 . Риск потери данных оказывается гораздо ниже, чем в случае с дорогим диском, а заплатите вы всего 60 % от его стоимости.
. Риск потери данных оказывается гораздо ниже, чем в случае с дорогим диском, а заплатите вы всего 60 % от его стоимости.
Несовместные события
Бросок кубика не может одновременно дать 4 и нечетное число. Вероятность получить либо 4, либо нечетное число, следовательно, равняется
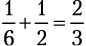 . Когда два события не могут произойти одновременно, они несовместные, или взаимоисключающие. Если вам нужно подсчитать вероятность любого из нескольких несовместных событий, просто просуммируйте их индивидуальные вероятности.
. Когда два события не могут произойти одновременно, они несовместные, или взаимоисключающие. Если вам нужно подсчитать вероятность любого из нескольких несовместных событий, просто просуммируйте их индивидуальные вероятности.
Выбор подписки
 Ваш интернет-сервис предлагает три тарифа: бесплатный, основной и профессиональный. Вы знаете, что случайный посетитель выберет бесплатный тариф с вероятностью 70 %, основной — с вероятностью 20 % и профессиональный — с вероятностью 10 %. Каковы шансы, что человек подпишется на платный тариф?
Ваш интернет-сервис предлагает три тарифа: бесплатный, основной и профессиональный. Вы знаете, что случайный посетитель выберет бесплатный тариф с вероятностью 70 %, основной — с вероятностью 20 % и профессиональный — с вероятностью 10 %. Каковы шансы, что человек подпишется на платный тариф?
Перечисленные события несовместны: нельзя выбрать и основной, и профессиональный тарифы одновременно. Вероятность, что пользователь подпишется на платный тариф, равняется 0,2 + 0,1 = 0,3.
Взаимодополняющие события
Выпавшее на кубике количество очков не может одновременно оказаться кратным трем (3, 6) и не делящимся на три, но оно определенно будет относиться к одной из этих категорий чисел. Вероятность получить результат, кратный трем, равняется
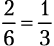 , следовательно, вероятность получить число, которое не делится на три, равняется
, следовательно, вероятность получить число, которое не делится на три, равняется
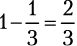 . Когда два несовместных события охватывают все возможные варианты, их называют взаимодополняющими, или соподчиненными. Сумма вероятностей взаимодополняющих событий равна 100 %.
. Когда два несовместных события охватывают все возможные варианты, их называют взаимодополняющими, или соподчиненными. Сумма вероятностей взаимодополняющих событий равна 100 %.
Игра «Защита башни»
 Ваш замок защищен пятью башнями. Каждая имеет 20 %-ную вероятность поразить захватчика, прежде чем он достигнет ворот. Каковы шансы остановить его?
Ваш замок защищен пятью башнями. Каждая имеет 20 %-ную вероятность поразить захватчика, прежде чем он достигнет ворот. Каковы шансы остановить его?
Вероятность поразить врага равна 0,2 + 0,2 + 0,2 + 0,2 + 0,2 = 1, или 100 %, верно? Неверно! Никогда не суммируйте вероятности независимых событий, не совершайте распространенной ошибки. Вместо этого используйте взаимодополняющие события дважды следующим образом.
• 20 %-ный шанс поразить врага — взаимодополняющий для 80 %-го шанса промахнуться. Вероятность того, что не попадут все башни, составляет 0,85 ≈ 0,33.
• Событие «все башни промахнулись» — взаимодополняющее для события «по крайней мере одна башня попала». Значит, вероятность остановить врага равна 1–0,33 = 0,67.
«Заблуждение игрока»
Если вы подбросили монету 10 раз и получили 10 «орлов», увеличилась ли от этого вероятность, что на 11-м броске выпадет «решка»? Или будет ли вероятность выигрыша в лотерею комбинации из шести последовательных чисел от 1 до 6 ниже, чем любой другой комбинации?
Не становитесь жертвой «заблуждения игрока»! Уже случившееся никак не влияет на результат независимого события. Никак. Никогда. В по-настоящему случайно разыгрываемой лотерее вероятность выпадения любого конкретного числа точно такая же, как любого другого. Нет никакой закономерности, согласно которой числа, редко выпадавшие в прошлом, должны чаще выпадать в будущем.
Более сложные вероятности
Можно было бы и дальше рассказывать о вероятности, но рамки раздела не позволяют этого. Всегда, занимаясь решением сложных задач, подыскивайте дополнительные инструменты. Вот пример.
И еще одно формирование команды
 23 человека хотят в вашу команду. В отношении каждого вы подбрасываете монету и принимаете его, только если выпадает «орел». Каковы шансы, что вы возьмете семь человек или меньше?
23 человека хотят в вашу команду. В отношении каждого вы подбрасываете монету и принимаете его, только если выпадает «орел». Каковы шансы, что вы возьмете семь человек или меньше?
Да, это трудно посчитать. Если вы будете долго искать в Интернете, то в конечном счете придете к биномиальному распределению. Вы можете визуализировать его в Wolfram Alpha
[21], набрав: B(23,l/2) <= 7.



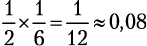 , или 8 %. Когда исход одного события не влияет на исход другого, их называют независимыми. Вероятность получить сочетание конкретных результатов двух независимых событий равна произведению вероятностей каждого из них.
, или 8 %. Когда исход одного события не влияет на исход другого, их называют независимыми. Вероятность получить сочетание конкретных результатов двух независимых событий равна произведению вероятностей каждого из них. Вам нужно организовать хранение данных в течение года. Один диск имеет вероятность сбоя 1 на 1 млрд. Другой стоит 20 % от цены первого, но в его случае вероятность сбоя — 1 на 2000. Какой диск вам следует купить?
Вам нужно организовать хранение данных в течение года. Один диск имеет вероятность сбоя 1 на 1 млрд. Другой стоит 20 % от цены первого, но в его случае вероятность сбоя — 1 на 2000. Какой диск вам следует купить?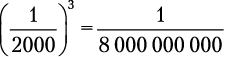 . Риск потери данных оказывается гораздо ниже, чем в случае с дорогим диском, а заплатите вы всего 60 % от его стоимости.
. Риск потери данных оказывается гораздо ниже, чем в случае с дорогим диском, а заплатите вы всего 60 % от его стоимости.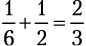 . Когда два события не могут произойти одновременно, они несовместные, или взаимоисключающие. Если вам нужно подсчитать вероятность любого из нескольких несовместных событий, просто просуммируйте их индивидуальные вероятности.
. Когда два события не могут произойти одновременно, они несовместные, или взаимоисключающие. Если вам нужно подсчитать вероятность любого из нескольких несовместных событий, просто просуммируйте их индивидуальные вероятности. Ваш интернет-сервис предлагает три тарифа: бесплатный, основной и профессиональный. Вы знаете, что случайный посетитель выберет бесплатный тариф с вероятностью 70 %, основной — с вероятностью 20 % и профессиональный — с вероятностью 10 %. Каковы шансы, что человек подпишется на платный тариф?
Ваш интернет-сервис предлагает три тарифа: бесплатный, основной и профессиональный. Вы знаете, что случайный посетитель выберет бесплатный тариф с вероятностью 70 %, основной — с вероятностью 20 % и профессиональный — с вероятностью 10 %. Каковы шансы, что человек подпишется на платный тариф?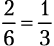 , следовательно, вероятность получить число, которое не делится на три, равняется
, следовательно, вероятность получить число, которое не делится на три, равняется
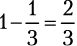 . Когда два несовместных события охватывают все возможные варианты, их называют взаимодополняющими, или соподчиненными. Сумма вероятностей взаимодополняющих событий равна 100 %.
. Когда два несовместных события охватывают все возможные варианты, их называют взаимодополняющими, или соподчиненными. Сумма вероятностей взаимодополняющих событий равна 100 %. Ваш замок защищен пятью башнями. Каждая имеет 20 %-ную вероятность поразить захватчика, прежде чем он достигнет ворот. Каковы шансы остановить его?
Ваш замок защищен пятью башнями. Каждая имеет 20 %-ную вероятность поразить захватчика, прежде чем он достигнет ворот. Каковы шансы остановить его? 23 человека хотят в вашу команду. В отношении каждого вы подбрасываете монету и принимаете его, только если выпадает «орел». Каковы шансы, что вы возьмете семь человек или меньше?
23 человека хотят в вашу команду. В отношении каждого вы подбрасываете монету и принимаете его, только если выпадает «орел». Каковы шансы, что вы возьмете семь человек или меньше?