A OR B: Вы пили.

A AND B: Вы пили и то и другое.

A XOR B: Вы пили, не смешивая.

Проверьте, правильно ли вы понимаете, как работают эти операторы. В табл. 1.1 перечислены все возможные комбинации двух переменных. Обратите внимание, что A
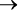 B тождественно! A OR B, а A XOR B тождественно!(A <—> B).
B тождественно! A OR B, а A XOR B тождественно!(A <—> B).
Таблица 1.1. Логические операции для четырех возможных комбинаций A и B
Булева алгебра
Булева алгебра
[10] позволяет упрощать логические выражения точно так же, как элементарная алгебра упрощает числовые.
Ассоциативность. Для последовательностей, состоящих только из операций AND или OR, круглые скобки не имеют значения. Так же, как последовательности только из операций сложения или умножения в элементарной алгебре, эти операции могут вычисляться в любом порядке.
A AND (B AND C) = (A AND B) AND C;
A OR (B OR C) = (A OR B) OR C.
Дистрибутивность. В элементарной алгебре мы раскрываем скобки: a × (b + c) = (a × b) + (a × c). Точно так же и в логике выполнение операции AND после OR эквивалентно выполнению операции OR над результатами операций AND и наоборот:
A AND (B OR C) = (A AND B) OR (A AND C);
A OR (B AND C) = (A OR B) AND (A OR C).
Правило де Моргана
[11]. Одновременно лета и зимы не бывает, поэтому у нас либо не лето, либо не зима. С другой стороны, оба выражения «не лето» и «не зима» истинны, если (и только) у нас не тот случай, когда либо лето, либо зима. Согласно этой логике, выполнение операций AND может быть сведено к операциям OR и наоборот:
!(A AND B) =!A OR! B;
!A AND!B =!(A OR B).
Эти правила позволяют преобразовывать логические модели, раскрывать их свойства и упрощать выражения. Давайте решим задачу.
Перегрев сервера
 Сервер выходит из строя из-за перегрева, когда кондиционирование воздуха выключено. Он также выходит из строя из-за перегрева, если барахлит кулер. При каких условиях сервер работает?
Сервер выходит из строя из-за перегрева, когда кондиционирование воздуха выключено. Он также выходит из строя из-за перегрева, если барахлит кулер. При каких условиях сервер работает?
Моделируя эту задачу в логических переменных, можно в одном выражении сформулировать условия, когда сервер выходит из строя:
A: Сервер перегревается.
B: Кондиционирование отключено.
C: Не работает кулер.
D: Сервер вышел из строя.
(A AND B) OR (A AND C)
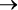 D.
D.
Используя правило дистрибутивности, выведем за скобки A:
A AND (B OR C)
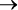 D.
D.
Сервер работает, когда! D. Противопоставление записывается так:
!D
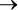 !(A AND (B OR C)).
!(A AND (B OR C)).
Применим правило де Моргана и раскроем скобки:
!D
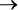 !A OR!(B OR C).
!A OR!(B OR C).
Воспользуемся правилом де Моргана еще раз:
!D
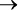 !A OR (!B AND!C).
!A OR (!B AND!C).
Данное выражение нам говорит, что когда сервер работает, мы имеем либо! A (он не перегревается), либо! B AND!C (все в порядке и с кондиционированием воздуха, и с кулером).
Таблицы истинности
Еще один способ анализа логических моделей состоит в сверке данных со всевозможными сочетаниями ее переменных. Каждой переменной в таблице истинности соответствует свой столбец. Строки представляют комбинации состояний переменных.






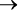 B тождественно! A OR B, а A XOR B тождественно!(A <—> B).
B тождественно! A OR B, а A XOR B тождественно!(A <—> B).
 Сервер выходит из строя из-за перегрева, когда кондиционирование воздуха выключено. Он также выходит из строя из-за перегрева, если барахлит кулер. При каких условиях сервер работает?
Сервер выходит из строя из-за перегрева, когда кондиционирование воздуха выключено. Он также выходит из строя из-за перегрева, если барахлит кулер. При каких условиях сервер работает?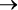 D.
D.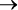 D.
D.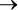 !(A AND (B OR C)).
!(A AND (B OR C)).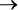 !A OR!(B OR C).
!A OR!(B OR C). !A OR (!B AND!C).
!A OR (!B AND!C).