Подведем итоги
В этой главе мы увидели приемы решения задач, не связанные с программированием непосредственно.
Раздел 1.1 объяснил, почему и как мы должны излагать мысли в письменной форме. Для наших задач мы создаем модели и применяем к ним концептуальные инструменты.
Раздел 1.2 познакомил с инструментами из булевой алгебры для работы с формальной логикой и таблицами истинности.
Раздел 1.3 показал важность теории вероятности и комбинаторики для решения задач разного рода. Быстрый приблизительный подсчет может показать вам, стоит ли браться за дальнейшие вычисления. Программисты-новички часто теряют время, анализируя слишком много сценариев.
Наконец, раздел 1.4 объяснил основные правила, позволяющие подсчитать вероятность чего-либо. Это бывает очень полезно при разработке решений, которые должны взаимодействовать с нашим дивным, но неопределенным миром.
Таким образом, мы в общих чертах обрисовали множество важных аспектов того, что ученые называют дискретной математикой. Еще больше интересного можно почерпнуть из приведенных ниже материалов или просто найти в «Википедии». Например, вы можете воспользоваться принципом Дирихле, чтобы доказать, что в Нью-Йорке по крайней мере у двух человек одинаковое число волос в шевелюре!
Часть из того, что мы здесь узнали, пригодится в следующей главе, где мы откроем для себя, возможно, самый важный аспект информатики.
Полезные материалы
• Дискретная математика и ее применения, 7-е издание (Discrete Mathematics and Its Applications, см. https://code.energy/rosen).
• Слайды профессора Жаннет Уинг, иллюстрирующие вычислительное мышление, см. https://code.energy/wing.
Глава 2. Вычислительная сложность
Практически любой расчет можно выполнить несколькими способами. Из них следует выбирать такие, которые позволяют выполнить вычисления за наименьшее время.
Ада Лавлейс
Сколько времени потребуется, чтобы разложить по порядку 26 перетасованных карт? А если у вас будет 52 карты, уйдет ли на эту же операцию вдвое больше времени? И насколько больше его потребуется на тысячу карточных колод? Ответ неразрывно связан с методом, который используется для сортировки карт.
Метод — это список однозначных команд, служащих для достижения цели. Метод, который всегда требует конечной серии операций, называется алгоритмом. Например, алгоритм сортировки карт представляет собой метод, где определены некие операции для сортировки колоды из 26 карт по масти и достоинству.
На меньшее количество операций нужно меньше вычислительной мощности. Нам нравятся быстрые решения, поэтому мы следим за числом операций в наших алгоритмах. В случае со многими алгоритмами необходимое число операций быстро растет с увеличением объема входных данных. В нашем случае может потребоваться всего несколько операций для сортировки 26 карт, но в четыре раза больше операций для сортировки 52 карт!
Чтобы избежать непредвиденных сложностей, связанных с раздуванием задачи, нужно узнать временную сложность алгоритма. В этой главе пойдет речь о том, как:
 рассчитывать и интерпретировать временные сложности;
рассчитывать и интерпретировать временные сложности;
 выражать их рост при помощи необычной нотации «О большое»;
выражать их рост при помощи необычной нотации «О большое»;
 избегать экспоненциальных алгоритмов;
избегать экспоненциальных алгоритмов;
 убедиться, что у вашего компьютера достаточно памяти.
убедиться, что у вашего компьютера достаточно памяти.
Но прежде нам предстоит узнать, как определяется временная сложность алгоритма.
Временная сложность записывается как: T(n). Она показывает количество операций, которые алгоритм выполняет при обработке входящих данных объема n. Также T(n) называют стоимостью выполнения алгоритма. Если наш алгоритм сортировки игральных карт подчиняется T(n) = n2, то мы можем предсказать, насколько больше потребуется времени, чтобы отсортировать колоду двойного размера:
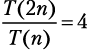 .
.
Надейтесь на лучшее, но готовьтесь к худшему
Будет ли быстрее отсортирована колода карт, которая уже почти упорядочена? Объем входящих данных — не единственная характеристика, влияющая на количество требуемых алгоритмом операций. Когда алгоритм может иметь разные значения T(n) для одного n, мы обращаемся к случаям, или, говоря по-другому, вариантам развития событий.
• Лучший случай — это ситуация, когда для любых входящих данных установленного объема требуется минимальное количество операций. В сортировке такое происходит, когда входящие данные уже упорядочены.
• Худший случай — когда для любых входящих данных данного объема требуется максимальное количество операций. Во многих алгоритмах сортировки такое случается, когда данные на входе передаются в обратном порядке.
• Средний случай предполагает среднее количество операций, обычно нужных для обработки входящих данных этого объема. Для сортировки средним считается случай, когда входящие данные поступают в произвольном порядке.
Худший случай — самый важный из всех. Ориентируясь на него, вы обеспечиваете себе гарантию. Когда ничего не говорится о сценарии, ориентируйтесь на худший случай. Далее мы узнаем, как на практике анализировать события c учетом худшего варианта их развития.

Рис. 2.1. Оценка времени
[22]



 рассчитывать и интерпретировать временные сложности;
рассчитывать и интерпретировать временные сложности; выражать их рост при помощи необычной нотации «О большое»;
выражать их рост при помощи необычной нотации «О большое»; избегать экспоненциальных алгоритмов;
избегать экспоненциальных алгоритмов; убедиться, что у вашего компьютера достаточно памяти.
убедиться, что у вашего компьютера достаточно памяти. .
.