Число ежегодных убийств в Англии и Уэльсе между 1998 и 2016 годами, а также 95-процентные доверительные интервалы для «истинного» уровня убийств
[183]
Итак, как же нам решить, произошло реальное изменение риска стать жертвой убийства или наблюдаемые изменения можно просто отнести к неизбежным случайным отклонениям? Если бы доверительные интервалы не перекрывались, то мы могли бы быть уверены, по крайней мере на 95 %, что изменение реально. Однако это довольно строгий критерий, и нам действительно следует построить 95-процентный интервал для изменения уровня убийств. Если такой интервал будет включать в себя 0, то мы не можем быть уверены в реальности изменения.
Между числом убийств за 2014–2015 и 2015–2016 годы произошло увеличение на 557–477 = 60. Оказывается, 95-процентный доверительный интервал для этого наблюдаемого изменения простирается от – 4 до +124. Это включает 0 (правда, едва-едва). Формально это означает, что мы не можем с 95-процентной уверенностью заключить, что истинный уровень изменился, но, поскольку нулевое значение находится на самом краю доверительного интервала, было бы неразумно утверждать, что изменений вовсе нет.
У доверительных интервалов вокруг числа убийств на рис. 9.4 совершенно иная природа по сравнению с погрешностями, скажем, для безработицы. Последние выражают нашу эпистемическую неопределенность в отношении фактического числа безработных, в то время как интервалы вокруг числа убийств не выражают неопределенности для их фактического количества (мы полагаем, что они подсчитаны верно), а относятся к истинным рискам убийств в обществе. Эти два вида интервалов могут похоже выглядеть и даже использовать одинаковую математику, однако их интерпретации принципиально разнятся.
В этой главе содержался довольно сложный материал, что неудивительно: фактически в ней заложен весь формальный фундамент для статистических выводов, основанных на вероятностном моделировании. Но усилия того стоят, поскольку теперь мы можем использовать эту конструкцию для выхода за рамки простых описаний и оценок характеристик мира и понимания того, как статистическое моделирование может нам помочь ответить на важные вопросы о реальном мироустройстве и таким образом обеспечить прочную основу для научных открытий.
Выводы
• Теорию вероятностей можно использовать для получения распределения для выборочных статистик, из которых могут быть выведены формулы для доверительных интервалов.
• 95-процентный доверительный интервал определяется так: если мы проведем большое количество независимых экспериментов, для которых верны определенные предположения, то в 95 % этих испытаний построенный доверительный интервал будет содержать истинное значение параметра. Нельзя утверждать, что какой-то интервал с вероятностью 95 % содержит истинное значение.
• Из центральной предельной теоремы следует, что для больших выборок выборочное среднее и некоторые другие статистики имеют приблизительно нормальное распределение.
• Погрешности обычно не включают систематическую ошибку, вызванную не стохастическими причинами, – для ее оценивания нужны внешние знания и рассуждения.
• Доверительные интервалы можно вычислять, даже если мы наблюдаем все данные. Они отражают неопределенность параметров базовой метафорической совокупности.
Глава 10. Отвечаем на вопросы и заявляем об открытиях
Рождается ли мальчиков больше, чем девочек?
Врач Джон Арбетнот, ставший в 1705 году придворным лекарем королевы Анны, задался целью ответить на этот вопрос и проанализировал данные об обрядах крещения, проведенных в Лондоне за 82 года – с 1629 по 1710 год. Результаты его исследования приведены на рис. 10.1 в виде соотношения полов, то есть числа родившихся мальчиков на 100 родившихся девочек.
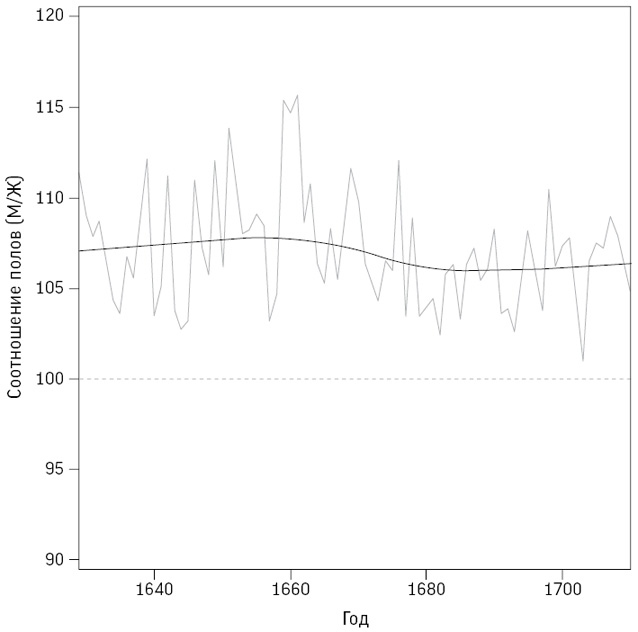
Рис. 10.1
Данные о соотношении полов (число мальчиков на 100 девочек) при обряде крещения в Лондоне между 1629 и 1710 годами, опубликованные Джоном Арбетнотом в 1710 году. Сплошная линия отображает равное число мальчиков и девочек; эта кривая построена по эмпирическим данным. Ежегодно мальчиков было окрещено больше, чем девочек
Арбетнот обнаружил, что ежегодно было окрещено больше мальчиков, чем девочек, причем соотношение колебалось от 101 до 116 и в целом составляло 107. Но он хотел вывести более общий закон, поэтому предположил, что если бы на самом деле никакой разницы между истинной долей мальчиков и девочек не было, то каждый год вероятность того, что мальчиков рождалось бы больше, чем девочек, а девочек рождалось бы больше, чем мальчиков, составила бы 50 на 50, то есть так же, как при подбрасывании монеты.
Но если предположить, что мальчики рождаются так же часто, как и девочки, и 82 года подряд наблюдается их избыток, то это все равно что 82 раза подбросить симметричную монету и каждый раз получить орла. Вероятность этого события составляет 1/282. Это очень маленькое число, с 24 нулями после запятой. Если бы мы наблюдали 82 выпадения орла в реальном эксперименте, то уверенно бы заявили, что монета нечестная. Точно так же и Арбетнот заключил, что некая сила заставляет рождаться больше мальчиков в целях компенсации повышенной смертности мужского пола: «Чтобы восстановить эти Потери, предусмотрительная Природа по промыслу мудрого Творца рождает больше Мужчин, чем Женщин; и это почти постоянное соотношение»
[184].
Впоследствии данные Арбетнота не раз перепроверялись. И хотя в них могут быть ошибки подсчета и учтены только англиканские
[185] обряды крещения, тем не менее его основной вывод по-прежнему верен: считается, что «естественное» соотношение полов – около 105, то есть на каждые 20 девочек рождается 21 мальчик. Название опубликованного им труда служит прямым статистическим подтверждением сверхъестественного вмешательства: «Аргумент в пользу Божественного провидения, извлеченный из постоянной регулярности, наблюдаемой при рождении обоих полов». И хотя Арбетнот тогда об этом не знал, он вошел в историю как человек, который выполнил первую проверку статистической значимости.
Пожалуй, мы подошли к самой важной части цикла решения проблем, где мы ищем ответы на конкретные вопросы о том, как устроен мир. Например:



