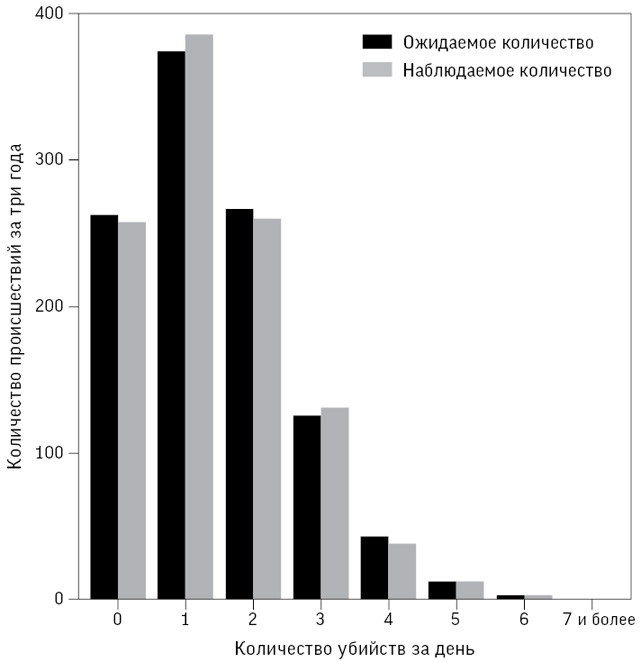
Рис. 8.5
Наблюдаемое и ожидаемое (при условии распределения Пуассона) ежедневное количество зарегистрированных убийств за 2014–2016 годы в Англии и Уэльсе
[167]
Чтобы ответить на вопрос, поставленный в начале этого раздела, мы можем вычислить вероятность семи и более убийств в день, исходя из распределения Пуассона. Она равна 0,07 %, а значит, такое событие можно ожидать в среднем раз в 1535 дней, то есть примерно раз в четыре года. Напрашивается вывод, что при нормальном ходе вещей оно маловероятно, но не невозможно.
Соответствие между этим математическим распределением и эмпирическими данными подозрительно хорошее. Несмотря на то что за каждой трагедией стоит какая-то личная история, и практически любая из них непредсказуема, данные ведут себя так, словно их сгенерировал какой-то известный случайный механизм. Благодаря способности представлять, что могли бы быть (но не были) убиты другие люди, мы наблюдаем один из множества возможных миров, которые могли реализоваться; точно так же как, подбрасывая монету, наблюдаем одну из возможных последовательностей.
Адольф Кетле – бельгийский статистик, социолог и астроном XIX века – одним из первых привлек внимание к потрясающей предсказуемости общей картины, составленной из отдельных непредсказуемых событий. Он был заинтригован появлением нормального распределения при различных явлениях (например, распределении веса новорожденного, как описывалось в главе 3) и предложил идею «среднего человека» (l’homme moyen), который вобрал в себя среднее значение всех характеристик. Кетле развил идею «социальной физики», поскольку регулярные закономерности социальной статистики, казалось, отражали какой-то почти механический процесс, лежащий в ее основе. Так же как случайные молекулы газа, соединяясь, обеспечивают предсказуемые физические свойства, непредсказуемые действия миллионов отдельных людей в совокупности генерируют национальный уровень самоубийств, который из года в год практически не меняется.
К счастью, нам незачем верить, что реальные события обусловлены чистой случайностью (что бы это ни было). Просто предположение о «случайности» заключает в себе всю неизбежную непредсказуемость мира или то, что иногда называют естественной изменчивостью. Поэтому мы установили, что вероятность образует надлежащий математический фундамент как для «чистой» случайности, проистекающей из субатомных процессов, монет, костей и так далее, так и для «естественной» неизбежной изменчивости, проявляющейся в весе новорожденных, уровне выживаемости после операций, результатах экзаменов, количестве убийств и других явлениях, которые нельзя точно предсказать.
В следующей главе мы обратимся к поистине замечательной теме: как объединить эти два аспекта вероятности, чтобы получить строгую основу для формальных статистических выводов.
Выводы
• Теория вероятностей предоставляет формальный язык и математические инструменты для работы со случайными явлениями.
• Вероятностные выводы не бывают интуитивно понятными, однако понимание можно улучшить с помощью идеи ожидаемого количества.
• Вероятности полезны даже тогда, когда нет явного применения механизма рандомизации.
• Многие социальные явления в целом демонстрируют удивительную закономерность, в то время как отдельные события совершенно непредсказуемы.
Глава 9. Объединяем вероятность и статистику
Предупреждение. Это, пожалуй, самая сложная глава в книге, но, проявив настойчивость и изучив ее, вы обретете ценное понимание статистических выводов.
Мы обнаружили, что в случайной выборке из 100 человек 20 – левши. Что можно сказать о доле левшей во всей генеральной совокупности?
В предыдущей главе мы обсуждали идею случайной величины – одного элемента данных, извлеченного из какого-то вероятностного распределения, описываемого определенными параметрами. Но нас редко интересует только один элемент – обычно у нас большой массив данных, для которого мы вычисляем среднее, медиану и другие статистики. Фундаментальный шаг, который мы сделаем в этой главе, – рассмотрим эти статистики как случайные величины, извлеченные из их собственных распределений.
Это существенный шаг, создавший проблемы не только поколениям статистиков, но и математикам, которые пытались выяснить, из каких распределений мы извлекаем эти статистики. С учетом обсуждения бутстрэппинга в главе 7 разумно задаться вопросом, зачем нам вообще нужна вся эта математика, когда мы можем узнать интервалы неопределенности и прочее, используя моделирование методом бутстрэппинга. Например, на вопрос, поставленный в начале главы, можно было ответить, взяв наблюдаемую выборку из 20 левшей и 80 правшей и многократные повторные выборки с возвратом по 100 наблюдений из этого набора, посмотреть на распределение наблюдаемой доли левшей.
Но такое моделирование неуклюже и затратно по времени, особенно для больших объемов данных, да и в более сложных ситуациях не так просто решить, что нужно моделировать. Напротив, формулы, предлагаемые теорией вероятностей, обеспечивают и понимание, и удобство и (в отличие от моделирования) всегда дают один и тот же ответ. Оборотная сторона в том, что эта теория опирается на предположения, и мы должны быть очень осторожны, чтобы впечатляющие выкладки не ввели нас в заблуждение и не привели к необоснованным выводам. Позже мы поговорим об этом подробнее, а пока, уже оценив полезность нормального и пуассоновского распределений, введем еще одно важное вероятностное распределение.
Предположим, что мы составляем выборки разного размера из совокупности, содержащей ровно 20 % левшей и 80 % правшей, и вычисляем вероятность получения различных возможных долей левшей. Конечно, здесь все наоборот – мы хотим по известной выборке узнать о неизвестной генеральной совокупности. Однако для этого нужно сначала исследовать, как известная совокупность порождает различные выборки.
Простейший случай – выборка из одного человека. Тогда доля леворуких будет 0 или 1 (в зависимости от того, выберем мы правшу или левшу) и вероятность этого события составит 0,8 и 0,2 соответственно. Полученное распределение вероятностей представлено на рис. 9.1(a).
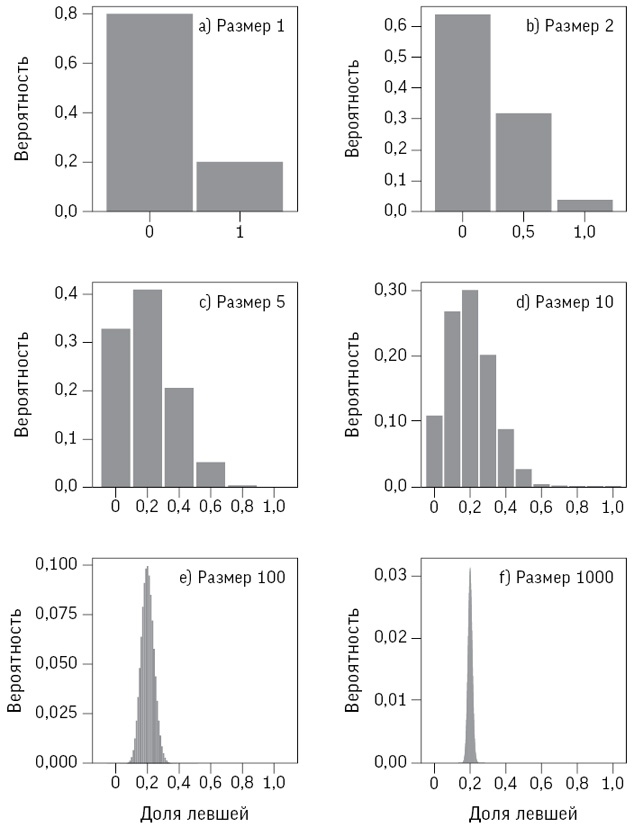
Рис. 9.1




