Можно указать еще одно замечательное семейство юристов, состоящее в родстве с Нортами, но место которого в родословной последних мне неизвестно, именно семейство Гайдов, заключающее в себе знаменитого первого графа Кларендона. По-видимому, лорд верховный судья Гайд дружески интересовался лордом хранителем печати Фрэнсисом Нортом, когда этот последний был еще только начинающим адвокатом и давал понять о своем родстве с ним, называя его «cousin».
Недостаток места, но никак не материала, вынуждает меня закончить этот перечень даровитых родственников семейств Нортов и Монтегю. Но я уверен, что и сказанного мною достаточно для подтверждения моего мнения, приведенного выше, что природные дарования чрезвычайно высокого разряда наследовались значительным числом членов этого семейства, которые таким образом своей репутацией были обязаны именно этим дарованиям, а не поддержке своих родственников.
Другой способ убеждения в наследственности даровитости заключается в наблюдении того, насколько ближайшие родственники весьма выдающихся людей являются более выдающимися, нежели родственники более отдаленные. Таблица II отчетливо решает этот вопрос уже объясненным мною путем. Она показывает, что близкие родственники судей гораздо даровитее дальних, и даже настолько, что родство в четвертой степени не имеет уже никакого заметного влияния на даровитость. Столбец С моей таблицы составлен на основании следующих данных: оказывается, что 23-м из числа упомянутых судей приписываются многочисленные семейства, в которых средним числом было по четыре взрослых сына; об этих 11 судьях говорится только, что они «имели потомство» – допустим, средним числом по 1,5 сына в каждом семействе; а у остальных общее число сыновей принимается приблизительно до 128; таким образом, общий итог будет равняться 294. К этому надо прибавить, что в 9 случаях говорится только, что судьи были женаты, но не упоминается о том, были ли у них дети; наконец, про 31 судью нам остается неизвестным – были ли они в браке. Я полагаю, эти данные дают право заключить, что судья, в среднем итоге, имел по крайней мере одного сына, достигавшего такого возраста, в котором он мог бы сделаться заметным, если бы обладал достаточной для этого даровитостью. Можно увидать также, что каждое взрослое семейство состоит средним числом не менее, как из 2,5 сыновей и из 2,5 дочерей, следовательно, каждый судья имеет средним числом 1,5 брата и 2,5 сестры.
Из этих данных легко определить число родственников в каждом порядке. Так, племянники состоят из сыновей братьев и сыновей сестер, а мы предположили, что у 100 судей должно быть 150 братьев и 250 сестер, из которых каждый брат и каждая сестра средним числом имеют по одному сыну, – следовательно 100 судей будут иметь 150 + 250, или 400 племянников.
Я не стану утруждать читателя дальнейшими расчетами. Достаточно сказать, что я разделил общее число выдающихся родственников 100 судей на число родственников в каждой степени, и это деление дало мне столбец Д таблицы II; тот же столбец я изображаю в генеалогическом порядке на таблице III.
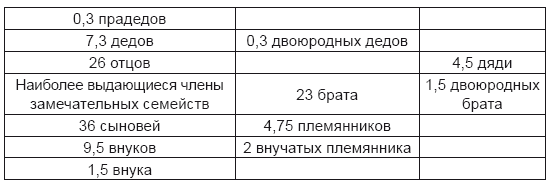
Следует заметить при этом, что таблица III относится только к прославившим себя семействам. Если бы мы привели ее в соответствие со столбцом Е таблицы II, в котором рассматриваются все судьи, независимо от того, имели ли они замечательных родственников или нет, тогда отношение между выдающимися родственниками в различных степенях родства осталось бы неизмененным, хотя абсолютное число уменьшилось бы приблизительно на одну треть.
Таблица III показывает несомненно, какое громадное влияние имеет близкий родственник для унаследования даровитости сравнительно с отдаленным. Говоря вообще, процентные отношения уменьшаются вчетверо с каждой отдаляющеюся степенью, как в нисходящей линии, так и в боковых. Так, если в первой степени родства процентное отношение было около 28, то во второй степени оно будет около 7, а в третьей 1,5.
Эта таблица удостоверяет еще другой факт, который обыкновенно считается маловероятным. Она показывает, что если мы обратим внимание на средние выводы из многих примеров, тогда частые капризы природы, при создании исключительных гениев, явятся скорее кажущимися, нежели действительно существующими. Талантливость обыкновенно не возникает внезапно и точно так же не исчезает разом; напротив того, она развивается постепенным и правильным отклонением от обычного жизненного уровня известной семьи. Статистика показывает, что существует правильное среднее повышение даровитости в поколениях, предшествующих высшей степени ее развития, и такое же правильное понижение в поколениях, последующих за этим моментом. В первом случае браки способствовали произведению талантливости, во втором же они были не способны поддержать ее.
После трех последовательных сочетаний с посторонними элементами потомство судей, по-видимому, утрачивает способность возвыситься до выдающегося положения. Эти результаты не удивительны, если их сравнить с более продолжительною родственною передачею черт лица или болезней. Для даровитости необходимо тройное основание, каждая опора которого должна быть прочно утверждена. Для того чтобы человек унаследовал даровитость в конкретном ее виде, он должен унаследовать три качества, отдельные и независимые одно от другого: именно, известную способность, энергию и силу. Если он не соединяет в себе всех этих трех качеств, или, по крайней мере, двух из них, он не может надеяться занять видное положение в свете. Вероятность, что человек наследует сочетание трех качеств, не имеющих никакой связи между собою, естественным образом втрое меньше вероятности, что он наследует одно из них.
Процент даровитости внуков судей представляет заметную разницу в тех случаях, когда сыновья судей (отцы этих внуков) были выдающимися личностями сравнительно с теми случаями, когда этого не было. Предположим, что сын судьи желает вступить в брак; спрашивается, какие он имеет шансы надеяться, что сыновья его сделаются впоследствии выдающимися людьми, опорою, а не обузою своей семьи?
Рассматривая те случаи, когда сын судьи сам был выдающимся человеком, я нахожу, что из 226 судей, живших до настоящего царствования, у 22 сыновья были замечательными людьми. Я не ввожу сюда примеров из настоящего царствования, так как внуки этих судей большею частью еще слишком молоды и не могли еще достигнуть известности. 22 на 226 представляет отношение 10 на 100 в виде процентного количества судей, имеющих выдающихся сыновей. (Читатель заметит, как близко этот результат подходит к числу 9,5, находящемуся в моей таблице, что одинаково говорит за общую верность обоих расчетов.) Из этих 22 я насчитываю следующие тройные сочетания. Семейство Аткинсов я считаю за две таких группы. Правда, дед их был только Главным судьей (chief justice) в северном Уэльсе, а не английским судьей; но сила крови в этом семействе сказалась не только в том факте, что сын его и двое внуков были английскими судьями, но и в том, что внук одного из них по женской линии также был английским судьей. Подобный же ряд представляете семейство Праттов, т. е. верховный судья, его сын, лорд канцлер, граф Кэмден, и внук, сын графа, первый маркиз Кэмден; последний был канцлером кембриджского университета и человеком замечательным во многих отношениях. Третий пример представляет семейство Йорков: сын лорда канцлера, графа Гардвика, Чарльз Йорк, был сам лордом канцлером. Сыновья его были даровитыми людьми: один из них был первым лордом адмиралтейства, другой – епископом Элским, третий отличился в военной службе и был пожалован бароном Дуврским, четвертый был замечательным адмиралом. Я не стану включать в свой счет всех этих примеров, но указываю на них, как на три удобные примера. Итак, в общей сложности мы имеем шесть благоприятных случаев; к ним мы имели бы полное право присоединить некоторых представителей замечательного семейства Монтегю, членами которого были многие из судей, как до восшествия на престол Карла I, так и после того. Но я желаю строго держаться указанных мною пределов, и потому из 22 примеров принимаю только шесть случаев успеха (на каждого судью я, как и прежде, полагаю только по одному сыну), или 1 случай на 4. Даже и при этих ограничениях вероятность того, что каждый из сыновей выдающегося сына судьи сделается замечательным человеком, есть не больше как 1 против 4.



