Баллы этих экзаменов никогда не публикуются, что составляет немалое неудобство для моей задачи. Для баллов этих не существует даже какой-либо одной общепринятой системы; каждому экзаменатору предоставляется придерживаться своих собственных цифр: но, каких бы цифр он ни придерживался, результаты по отношению к сравнительному достоинству будут одни и те же. Один из кембриджских экзаменаторов обязательно снабдил меня копией с двух своих экзаменационных списков, в которых система баллов настолько сходна, что с помощью небольших соответственных изменений представляется легкая возможность сравнения их. Документы эти были сообщены мне до известной степени конфиденциально, поэтому я не имею права опубликовать их в таком виде, какой указывал бы на года, к которым относятся эти отметки. Я привожу их просто как группы знаков, наглядно показывающие громадную разницу в степенях способности. Последний студент из этого списка получает менее 300 баллов; последний из соискателей (wranglers) получает около 1500 баллов, между тем как старший соискатель в одном из списков, лежащих передо мною, получил более 7500 баллов. Следовательно, достоинство худшего из соискателей превосходит более чем в пять раз достоинство худшего из студентов, удостоившихся отличий, и составляет менее чем пятую долю достоинства старшего wrangler’a.
Таблица степеней достоинства студентов, получающих отличие за успехи в математике в кембриджском университете.
Результаты обоих годов соединены в одну таблицу.
Высшая сумма баллов, которую можно было получить, простиралась до 17 000.
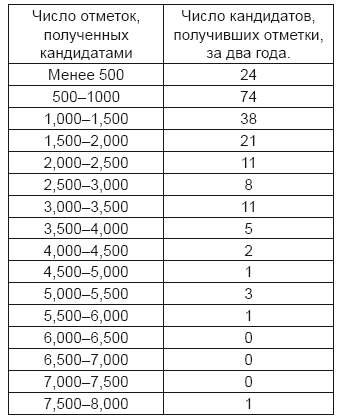
Полное число баллов, полученных старшим wrangler’oм в наиболее замечательном из двух этих годов, было 7634; второй wrangler в том же году получил 4123, а последний студент в списке отличившихся получил только 237. Следовательно, старший соискатель получил почти вдвое больше баллов, чем второй, и слишком в тридцать два раза более, чем последние из студентов списка. От другого экзаменатора я получил отметки одного года, в котором старший wrangler особенно выдавался между всеми остальными. Он получил 9422 балла, между тем как второй соискатель того же года, достоинства которого никак не уступали достоинствам вторых wrangler’oв вообще, получил только 5642. Последний же студент того же списка имел только 309 баллов, или одну тридцатую числа полученного старшим соискателем. Я имею также некоторые подробности касательно четвертого, в высшей степени замечательного года, в котором старший wrangler получил в целых десять раз более баллов, чем второй. Между тем я расспрашивал опытных экзаменаторов о том, насколько цифры баллов могут считаться верным выражением силы данного кандидата в математике, и все они высказывали такого рода мнения, что цифры эти со строгою точностью выражают силу кандидатов низших разрядов, но по отношению к высшим представляют такую оценку, которая всегда остается ниже их действительных достоинств. Другими словами, старшие wrangler’ы о которых я упоминал выше, превосходили своими способностями более, чем в тридцать или тридцать два раза низших из кандидатов, попавших в списки отличившихся. Они могли бы справиться с задачами более чем в тридцать два раза труднейшими, или же, имея дело с задачами одинаковой трудности, но доступными пониманию всех, решили бы их с быстротой, которая, быть может, представляла бы квадратный корень этого отношения. Можно предположить с достаточной основательностью, что экзаменационные отметки не могут воздавать полной справедливости лучшим из кандидатов, так как большая часть времени на экзаменах поглощается чисто механическим процессом писанья. Каждый раз, как мысль кандидата опережает его перо, он ничего не выигрывает от большей быстроты своего соображения. Однако должно упомянуть, что многие из наиболее способных студентов могут выказать свое превосходство и при непродолжительном письменном изложении. В задачах, предлагаемых им для решения, они сразу находят путь к самому корню вопроса и, доказав немногими отчетливыми, верными и сильными штрихами свою способность справиться с трудностью его, переходят к другому вопросу. Каждое слово у них говорит само за себя. Так покойный Г. Лесли Эллис, который был блистательным старшим wrangler’ом в 1840 г. и имя которого хорошо известно многим поколениям кембриджских студентов, как имя человека, обладавшего изумительно сильными, всеобъемлющим умом, – не мог оставаться даже в экзаменационном зале во все продолжение испытания: здоровье его было слабо и ему нужно было беречь свои силы.
Математические способности последнего студента в списке отличившихся, представляющиеся такими слабыми в сравнении со способностями старшего wrangler’a, являются посредственными, или даже стоящими выше посредственности, если их сравнить со способностями англичан вообще. Хотя экзамен ставит 100 отличных студентов выше, в то же время он ставит не менее трехсот студентов ниже этого уровня. Если даже мы допустим, что из этих трехсот двести не хотят работать настолько усидчиво, насколько это нужно для получения отличия, все же остаются еще сто, которые, если бы даже и работали со всевозможною усидчивостью, не могли бы добиться отличий. Каждый знает, как большинство людей мало способны к отвлеченным представлениям, хотя бы самого немудреного свойства, – как слаб и нерешителен их прием в умственной работе, как легко они впадают в затруднения, как мало доступно для них точное и основательное знание. Людям, хорошо знакомым с какою-нибудь отраслью науки, нередко приходится выслушивать, как мужчины и женщины посредственных способностей передают друг другу сведения, вынесенные ими об этом предмете из какой либо лекции, – положим, в Royal Institution, где они высидели целый час, слушая с восторженным вниманием изумительно ясное изложение, сопровождаемое самыми удивительными и превосходно исполненными опытами; всем этим они остались в высшей степени довольны и, по собственному их уверению, вынесли оттуда множество новых сведений. А между тем положительно тяжело слушать, когда они рассказывают о слышанном и виденном ими. Воспоминания их являются в виде какого-то хаоса туманных или фальшивых представлений, которым только их собственное воображение дает некоторую определенную форму, не имеющую ничего общего с тем, что лектор хотел сказать. Средний уровень понимания даже так называемой просвещенной публики, если его подвергнуть строгой проверке, окажется низким до смешного.
Говоря о различиях между людьми, мы ни одной минуты не должны держаться ошибочного предположения, будто математики по необходимости отличаются односторонностью своих природных дарований. Многие примеры именно убеждают нас в противном; из этих примеров я укажу на нижеследующие, приводимые мной как доказательства наследственности таланта в приложении к главе «Ученые». Более всего я указываю на Лейбница, как на человека, обладавшего самыми разносторонними умственными дарованиями; но и Ампер, Араго, Кондорсе и Даламбер пользуются известностью не только в качестве математиков. И даже с тех пор, как программа кембриджских экзаменов настолько расширена, что кроме математики обнимает еще и другие предметы, различие в способностях между высшими и низшими из кандидатов, удостаивающихся отличия, проявляется еще резче, чем в вышеописанных мною случаях. Мы по-прежнему, с одной стороны, находим людей посредственного дарования, вся энергия которых поглощается усилием, необходимым для того, чтобы получить свои 237 баллов за математику; но с другой стороны, мы имеем небольшую группу старших wrangler’ов, которые в то же время проявляют замечательные способности в изучении классических и многих других предметов. Кембридж представляет несколько таких примеров. Его списки отличий по классическим наукам ведутся еще слишком недавно, но доказательства того мы найдем и за прежнее время. Так, доктор Джордж Ботлер, бывший директором Харроуского училища в течение многих лет, включая и тот период, когда Байрон был воспитанником этого училища (настоящий директор в Гарроу – сын этого Ботлера; двое из других его сыновей также стоят во главе больших среднеучебных заведений), – получил этот классический пост, без сомнения, благодаря своему обширному классическому образованию. Между тем доктор Ботлер был старшим учителем в 1794 г., в том самом году, когда лорд канцлер Линдгерс получил отличие второго wrangler’a. Покойный доктор Кэй, епископ Линкольнский, и покойный сэр Э. Альдерсон, судья, – оба были старшими wrangler’aми и в то же время получили в своем курсе первые награды за успехи в классических предметах. После 1824 г., когда впервые были введены классические испытания, покойный мистер Гоборн (двоюродный брат доктора Гоборна, Норвического декана, и племянник известного юриста Гоборна) был вторым wrangler’oм в 1835 г. и в том же году получил первую награду за классицизм. Но в более близкие к нам времена приготовительная работа, необходимая для того, чтобы достигнуть высшего отличия по математике, разрослась до таких громадных размеров, что большая специализация научных занятий стала неизбежной. Теперь студенту прямо недостает времени для приобретения познаний, необходимых для занятия первого места более чем по одной отрасли наук. Впоследствии мы уже не видим более примеров, чтобы молодой человек являлся абсолютно первым на обоих испытаниях, хотя и можно найти несколько примеров высокой степени отличия, достигаемой одним и тем же лицом и в математике и в классических предметах, в чем легко убедиться, просмотрев списки, опубликованные в «Кембриджском Календаре». Наибольшее из этих отличий последнего времени, по-видимому, выпало на долю доктора Барри, бывшего директором Чельтенгемского училища и состоящего теперь директором Королевской Коллегии в Лондоне (сын известного архитектора, сэра Чарльза Барри, и брат Эдуарда Барри, который наследовал профессию своего отца). Он был в своем курсе четвертым по математике и седьмым по классическим наукам.



