Еще один пример включает уже прямое столкновение между Дженокки и Пеано. Лекции Дженокки по дифференциальному и интегральному исчислению высоко ценились в университете, и в 1883 г. Пеано попытался уговорить старшего коллегу собрать их в книгу. Дженокки отказался, отговорившись плохим здоровьем, но Пеано сказал, что может сам написать книгу от имени Дженокки. Книга Анджело Дженокки под названием «Дифференциальное исчисление и начала интегрального исчисления» (Calcolo differenziale e principii di calcolo integrale) вышла в конце 1884 г. с примечанием: «С добавлениями д-ра Джузеппе Пеано».
Это издание породило, по крайней мере поначалу, небольшой скандал. Пеано не только собрал и скомпилировал лекции Дженокки, но и включил в книгу то, что сам он назвал «важными добавлениями». Эта формулировка производила впечатление одновременно эгоизма и неуважения к человеку, обозначенному в книге как автор. Как может молодой выскочка улучшить работу мастера? Сам Дженокки тоже сначала рассердился, хотя со временем он, кажется, в целом оценил книгу по достоинству. Задним числом можно сказать, что добавления были очень важными.
Несмотря на довольно нахальный подход Пеано к самопродвижению — или, скорее, отчасти благодаря ему — он стремительно двигался по карьерной лестнице и набрал влияние. В 1886 г. Пеано занял второй пост профессора в Королевской военной академии, а в 1890 г. получил пожизненный пост профессора в Турине. Именно в этот период он опубликовал свои самые интересные и важные работы. Одним из величайших его достижений было формулирование того, что мы сегодня называем аксиомами Пеано, — небольшого набора простых утверждений, описывающих все свойства натуральных чисел (0, 1, 2, 3, …). Он также был разработчиком и пропагандистом формального стандартизованного «языка», который можно использовать для формулирования математических утверждений. Этот язык позволяет резко сократить математические доказательства, которые зачастую бывают чрезмерно громоздкими. Нотация Пеано до сих пор используется в почти неизменном виде. В 1890 г. он стал одним из основателей журнала Rivista di Matematica, в котором опубликовал свою первую «кошачью» статью «Принцип площадей и история кошки», а в 1891 г. начал «Стандарты проектов» (Formulario Project), целью которой было создание стандартизованной энциклопедии математики с использованием разработанного им символьного языка.
Еще один образец работы Пеано стоит того, чтобы упомянуть его здесь: это концепция заполняющей пространство кривой. Идею такой кривой представим вопросом: можно ли нарисовать одну-единственную кривую, которая полностью заполняет квадрат? Если говорить о карандаше и бумаге, то мы всегда можем заполнить квадрат, поскольку кончик грифеля имеет конечную толщину. Однако в математике линия — это объект, имеющий длину, но не имеющий ширины, тогда как квадрат имеет и длину, и ширину. Интуитивно нам представляется, что в этом смысле квадрат «больше», чем линия. Мы часто характеризуем это, называя размерности объектов: линия — одномерный объект, а квадрат — двумерный.
К концу XIX в. развитие математики позволило продемонстрировать, что число идеальных точек в линии и квадрате совершенно одинаково. Это значит, в принципе, что квадрат можно заполнить одной непрерывной линией, и именно Пеано первым показал в явном виде, как это сделать. Конструкция, которую он использовал, показана на рисунке, где квадрат заполняется линией, описывающей все более извилистую траекторию. На первом шаге траектория имеет попросту S-образную форму. В следующей итерации на отдельных участках траектории делаются свои S-образные ответвления, в следующей — ответвления на участках ответвлений и т. д. Пеано сумел строго доказать, что, произведя такую операцию бесконечное число раз, мы получим единую неразрывную линию, проходящую через каждую точку квадрата — мало того, проходящую через каждую точку не по одному разу.
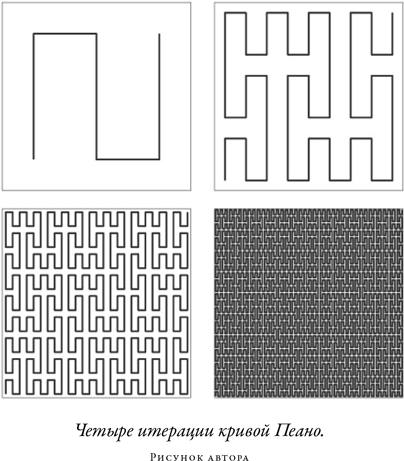
Много позже математики поймут, что Пеано открыл весьма любопытный образец интереснейшего математического объекта — фрактала. Обычные геометрические объекты имеют размерности, задаваемые не дробными числами, — квадрат двумерен, тогда как линия одномерна, — и у каждого объекта это число является, в определенном смысле, мерой того, сколько пространства занимает объект. Фракталы — объекты с дробной размерностью, и это указывает на то, что занимаемое фракталом количество пространства принципиально отличается от количества пространства, занимаемого простыми объектами. К примеру, фрактал с размерностью 1,5 занимает больше пространства, чем линия, но меньше, чем квадрат. Фракталы часто описывают как объекты, которые на любом уровне увеличения выглядят в основном одинаково — примерно как тонкий срез ветки дерева с виду похож на толстый срез ветки. Это самоподобие присутствует и в кривой Пеано. В общем, Пеано в своей необычной конструкции обнаружил необычный фрактал с фрактальной размерностью, равной 2, — не дробный фрактал.
Как мы уже видели, Пеано был амбициозным и изобретательным математиком, которого, как правило, интересовали крупные проекты. Однако он также всегда стремился показать, что серьезные математические инструменты, которыми он пользовался, применимы и к решению реальных практических задач. Обдумав на протяжении некоторого времени проблему падающей кошки, он увидел в ней объяснение одной из геофизических задач, вызывавших в то время большой интерес, — чандлеровского колебания полюсов.
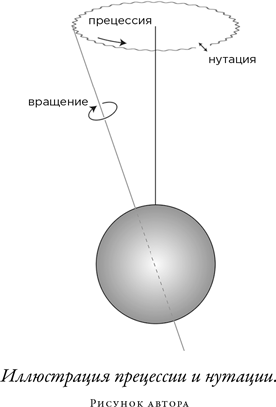
Ко времени Пеано астрономы уже поняли, что направление оси вращения Земли не постоянно. Подобно оси вращающегося волчка или гироскопа, эта ось описывает своим концом окружность, что называется прецессией. Полный цикл прецессии земной оси составляет 26 000 лет. На пути своем ось слегка колеблется, или претерпевает нутацию, с периодом 18,6 года. Прецессия и нутация вызываются взаимодействием Земли с гравитационными силами Солнца и Луны.
Еще одну форму нутации предсказал в 1765 г. математик Леонард Эйлер. Он предположил, что сфероидальная (слегка несферическая) форма Земли допускает «свободную нутацию»: дополнительные небольшие колебания земной оси по отношению к твердой Земле, которая автономна и не подвержена действию внешних сил. Эти колебания возникают потому, что ось симметрии Земли слегка отличается от ее же оси вращения. После некоторой замечательной математической гимнастики Эйлер предсказал, что эта свободная нутация должна иметь период 306 суток.
Ожидалось, что такие колебания должны представлять собой чрезвычайно маленькие изменения в направлении земной оси; для их регистрации требовались тщательные измерения положения звезд в том виде, как они видны с Земли, на протяжении по крайней мере года. Такие серьезные препятствия ученые рассматривают как вызов для себя, и на протяжении более чем 100 лет многочисленные исследователи пытались наблюдать предсказанную Эйлером свободную нутацию. Никто из них не добился успеха, и к 1880-м гг. астрономы, в сущности, сдались и отказались от поисков этого эффекта.




