1. Все планеты движутся вокруг Солнца по эллипсу, в одном из фокусов которого находится Солнце.
2. Радиус-вектор от Солнца до планеты «заметает» равные площади в равные интервалы времени.
3. Квадраты времен обращения двух планет пропорциональны кубам больших полуосей их орбит: T2 ~ a3.
§ 3. Развитие динамики
В то время, когда Кеплер открывал эти законы, Галилей изучал законы движения. Он пытался выяснить, чтó заставляет планеты двигаться. (В те дни одна из предлагавшихся теорий утверждала: планеты движутся потому, что за ними летят невидимые ангелы, которые взмахами своих крыльев гонят планеты вперед. Ныне эта теория, как вы вскоре увидите, несколько видоизменена! По-видимому, чтобы заставить планеты вращаться, невидимые ангелы обязаны витать во всевозможных направлениях и обходиться без крыльев. В остальном эти теории схожи!) И Галилей открыл одно знаменательное свойство движения, достаточное, чтобы понять эти законы. Это – принцип инерции: если при движении тела его ничто не касается, ничто не возмущает, то оно может лететь вечно с постоянной скоростью и по прямой. (А почему это так? Мы этого не знаем, но так уж оно повелось.)
Ньютон затем видоизменил эту мысль, говоря, что единственный способ изменить движение тела – это применить силу. Если тело разгоняется, значит сила была приложена в направлении движения. Если тело повернуло в сторону, то сила была приложена сбоку. Если, например, привязать камень к бечевке и вертеть им по кругу, то, чтобы удержать его на окружности, нужна сила. Мы должны все время натягивать бечевку. Закон состоит в следующем: ускорение, производимое силой, обратно пропорционально массе. Или иначе: сила пропорциональна массе и ускорению. Чем массивнее тело, тем бóльшая сила необходима, чтобы создать нужное ускорение. (Массу можно измерить, привязав к веревке другой камень и вертя им по тому же кругу с той же скоростью. Так можно обнаружить, что массивным телам нужна бóльшая сила.) Из этих рассуждений последовала блестящая мысль: чтобы удержать планету на ее орбите, никакой касательной силы не нужно (ангелам нет нужды летать по касательной), потому что планета и так будет лететь в нужном направлении. Если бы ничего ей не мешало, она бы удалилась по прямой линии. Но истинное движение уклоняется от этой прямой и отклоняется как раз поперек движения, а не по движению. Иными словами, благодаря принципу инерции сила, потребная для управления движением планет вокруг Солнца, это не сила, вращающая их вокруг Солнца, а сила, направленная к Солнцу (ну а раз сила направлена к Солнцу, то, бесспорно, это и есть тот самый ангел!).
§ 4. Ньютонов закон тяготения
Лучше других поняв природу движения, Ньютон прикинул, что именно Солнце может явиться источником, штаб-квартирой сил, управляющих движением планет. Он убедился (вскоре, быть может, убедимся в этом и мы), что «заметание» равных площадей в равные интервалы времени есть верный знак того, что все отклонения от прямой в точности радиальны, или что закон площадей есть прямое следствие того, что все силы направлены точно к Солнцу.
Кроме того, из анализа третьего закона Кеплера можно вывести, что чем дальше от Солнца планета, тем слабее сила. Из сравнения двух планет на разных расстояниях следует, что силы обратно пропорциональны квадратам относительных расстояний. Сочетая оба закона, Ньютон пришел к заключению, что должна существовать сила, обратная квадрату расстояния и направленная по прямой между Солнцем и планетой.
Будучи человеком, склонным к обобщениям, Ньютон, конечно, предположил, что эта связь применима не только к Солнцу, удерживающему планеты, но что она носит более общий характер. Уже было известно, к примеру, что вокруг Юпитера обращаются луны, подобно тому как Луна ходит вокруг Земли, и Ньютону казалось естественным, что и планеты силой держат свои луны возле себя. Тогда он уже знал о силе, удерживающей нас на Земле, и предположил, что эта сила всеобщая и что все притягивается ко всему.
Тогда он спросил себя: притягивает ли Земля людей так же, как Луну («так же» значит обратно пропорционально квадрату расстояния). Если тело у поверхности Земли падает в первую секунду (из состояния покоя) на 4,9 м, то на сколько падает Луна? Можно возразить, что Луна вообще не падает. Но если бы на Луну не действовала сила, она бы унеслась по прямой линии, а на самом деле она обращается по круговой орбите; следовательно, она падает с того места, где она должна была бы быть, если бы сила на нее не действовала. Зная радиус орбиты Луны (около 384 000 км)и время ее оборота вокруг Земли (около 29 дней), можно подсчитать, сколько она проходит за 1 сек и затем на сколько за это время она падает
[9]. Оказывается, что это расстояние примерно равно 1,36 мм. Это хорошо укладывается в закон обратных квадратов, потому что радиус Земли 6370 км, и если на этом расстоянии тела, падая, проходят в первую секунду 4,9 м, то на расстоянии в 384 тыс. км, т. е. в 60 раз дальше от центра Земли, они должны падать на 1/3600 от 4,9 м, или как раз на 1,36 мм. Желая подтвердить свою теорию тяготения подобными расчетами, Ньютон их аккуратно проделал и… получил сильнейшее несовпадение цифр. Он счел, что теория противоречит фактам, и не опубликовал ее. Шестью годами позже новые измерения радиуса Земли показали, что принятое в ту пору астрономами расстояние до Луны было неверным. Услышав об этом, Ньютон провел новый расчет с исправленными цифрами и получил уже превосходное совпадение.
Мысль, что Луна «падает», несколько смущает; почему же она тогда не приближается? Эта мысль настолько интересна, что заслуживает дальнейшего пояснения: Луна «падает» в том смысле, что отклоняется от прямой линии, по которой она бы двигалась, не будь больше никаких сил.
Рассмотрим другой, уже чисто земной пример. Тело, выпущенное из рук у земной поверхности, упадет в первую секунду на 4,9 м. Тело, брошенное горизонтально, также падает на 4,9 м.
На фиг. 7.3 показан прибор, демонстрирующий это явление.
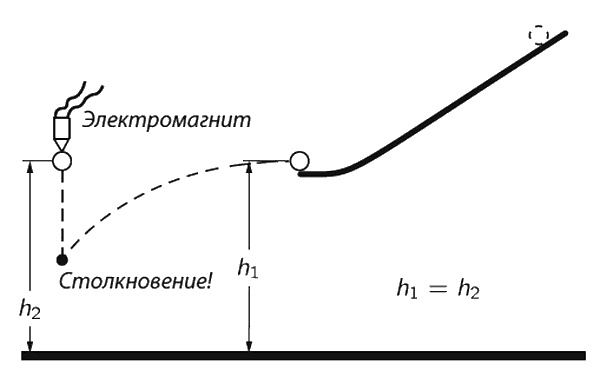
Фиг. 7.3. Прибор для демонстрации независимости вертикальных и горизонтальных движений.
Из горизонтального желоба выскакивает и летит вперед шарик. С той же высоты вертикально падает вниз другой шарик (имеется электрическая схема, выпускающая второй шар как раз в тот момент, когда первый соскальзывает с желоба). Они сталкиваются в воздухе, т. е. это значит, что они за одинаковое время снижаются одинаково. Пуля, выпущенная горизонтально, может пройти за 1 сек даже полкилометра, а вниз за это время она упадет на 4,9 м. Что случится, если пуля будет вылетать из ствола все быстрее? Не забудьте, что поверхность Земли кривая. Пуля может вылететь с такой скоростью, что, упав на 4,9 м, она все равно останется по отношению к Земле на первоначальной высоте. Может ли такое быть? Да; хотя она падает, но и Земля искривляется, вот и получается падение «вокруг» Земли. Надо только узнать, на каком расстоянии поверхность Земли окажется на 4,9 м ниже горизонта. На фиг. 7.4 изображена Земля с ее радиусом (6370 км)и касательный прямой путь пули (в отсутствие сил). Остается вспомнить одну из занятных геометрических теорем о том, что длина полухорды, перпендикулярной диаметру, равна среднему геометрическому между длинами отрезков диаметра. Значит, расстояние, пройденное пулей, есть среднее пропорциональное между 4,9 м падения и 12 740 км диаметра Земли, т. е.



